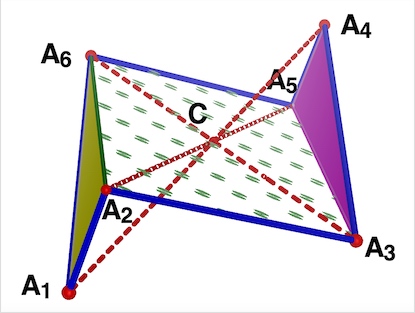

Theorem: In 3D space, if the opposite sides of a spatial 3D hexagon are parallel, then the opposite sides are equal; i.e. the formed spatial figure is a 3D parallelo-hexagon.
Corollary: Unlike the plane, where it's possible to construct a hexagon with opposite sides parallel, but not necessarily equal, the above theorem proves the surprising result that this is impossible for a hexagon in 3D space.
Illustration: Above is a short video clip that briefly & dynamically illustrates the 3D parallelo-hexagon using Cabri 3D.
One can think of the 3D parallelo-hexagon as consisting of 3 different planar 2D parallelograms in space, all three intersecting in a single point; i.e. its point of symmetry.
More Info
a) For more background & proofs, read the paper by Heinz Schumann (University of Weingarten, Germany) & myself in the July 2018 issue of 'The Mathematical Gazette', which is available at:
b) Below is a photo of a folded paper model of a 3D-parallelo-hexagon.

Notes:
1) The 3D parallelo-hexagon has a point of (reflective) symmetry like the 2D parallelogram, but unlike the 2D parallelogram, it does NOT have half-turn symmetry.
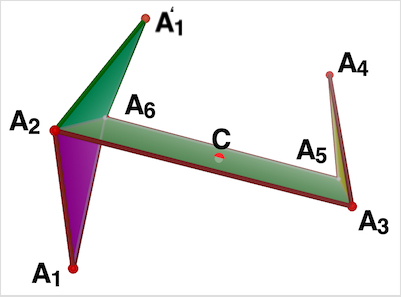
2) The converse of the theorem above is false. Having opposite sides equal for a spatial 3D hexagon is a necessary, but not sufficient condition. One can easily construct a counter-example as shown below from the original 3D parallelo-hexagon. By reflecting A1A2A6 in the plane on which parallelogram A2A3A5A6 lies, a new spatial 3D hexagon A'1A2A3A4A5A6 is obtained, which clearly still has the pairs of opposite sides equal, but A'1A2 is no longer parallel to opposite side A4A5, and inclined at angle. Similarly, A'1A6 is also no longer parallel to opposite side A3A4.
A 3D parallelo-hexagon is also formed by the centroids of the triangles subdividing a spatial 3D hexagon. See for example:
*************************
Michael de Villiers, created 6 January 2019; updated 17 August 2021.