For this activity, click on Online LOGO (Turtle) geometry to open this free online applet in a new window. Try to resize the windows a little so you have them more or less alongside each other.
With this nice applet you can program an arrow to move FORWARD with the command 'fd', and turn it LEFT or RIGHT through any angle in degrees you choose with the respective commands 'lt anglesize' or 'rt anglesize', to DRAW an endless variety of geometric figures. Read the Instructions about the available commands on the left.
Instructions:
1) In the active window of the open applet, type the following commands one after the other, pressing GO each time, to move the arrow FORWARD by 10 steps and then TURNING it RIGHT through 144 degrees, and repeating it another 4 times. Can you guess in advance what type of polygon will be formed?
fd 10
rt 144
fd 10
rt 144
fd 10
rt 144
fd 10
rt 144
fd 10
rt 144
2) What type of polygon is formed? Is that what you expected? Can you figure out the sum of its
interior angles?
3) To draw a new figure, type in 'cs' at the bottom and click GO to clear the screen. Try drawing an equilateral triangle, a square, a regular convex pentagon, etc. Or try
repeating these procedures a number of times and see what figures you get: forward 8
right turn 135; forward 8 right turn 160; forward 8 right turn 80, etc. Can you
figure out the sum of the interior angles of each of these figures?
4) What will the sum of the interior angles be if the
polygon in 2), or any of the others, are irregular, and do not
have equal sides and angles? Will their interior angle sum change or be
the same? Continue below or investigate further using suitable dynamic geometry
software.
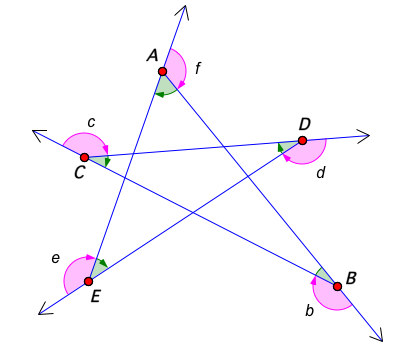
1a) You may have earlier learnt the formula S = 180(n-2) by which to determine the interior angle sum of a polygon in degrees, but this formula is only valid for simple convex and concave polygons, and NOT valid for a star pentagon like the one shown below.
1b) From Activity 1, no. 2, make a conjecture regarding the interior angle sum of a general star pentagon. Click on the 'Show Angle Sum' below to check the interior angle sum for a star pentagon like ABCDE.
Star pentagon and other crossed polygons
1c) Drag vertices A, B, C, D or E. What do you notice about the Angle Sum of the star pentagon? Can you explain (prove) it?
1d) Though there are several different ways of proving the interior angle sum of a star pentagon like this, try reasoning from rotating a pencil by the exterior angle at each vertex in order, and counting the total number of full revolutions it undergoes, moving completely around the figure until facing in the same starting direction.
Challenge: Can you find a general formula in terms of the number of vertices of the polygon as well as the number of full revolutions one undergoes, moving completely around the figure, by which to easily find the interior angle sum of the star pentagon above, as well as for the following polygons, namely, a crossed septagon, crossed octagon and a crossed quadrilateral?
1) Click on the appropriate Link to ... in the dynamic sketch above to check the interior angle sum for a crossed septagon like ABCDEFG. Then drag the septagon into other shapes and see if you can correctly predict or explain the shown interior angle sum.
2) Click on the appropriate Link to ... in the dynamic sketch above to check the interior angle sum of a crossed octagon like HIJKLMNO. Then drag the octagon into other shapes and see if you can correctly predict or explain the shown interior angle sum.
3) Click on the appropriate Link to ... in the dynamic sketch above to check the interior angle sum for a crossed quadrilateral like PQRS. Then drag the quadrilateral into the shape of a convex or concave quadrilateral (e.g. dragging S to the left across PQ), and then back again into a crossed shape. Can you explain (prove) what you observe? Why does the crossed quadrilateral have two reflexive angles? (Hint: consider directed angles by Evan Chen. The linked pdf also explains how, using directed angles, one can write solutions to math olympiad problems that cover all cases).
Notes & References
a) My 2012 book Rethinking Proof with Sketchpad has a learning activity with a worksheet and associated sketch in relation to the defining of 'interior angles' in terms of the concept of 'directed angles' so as to extend it in a consistent way to the interior angle sum of a crossed quadrilateral, and crossed polygons in general.
b) Read my 1989 IJMEST article From 'TO POLY' to generalized poly-figures and their classification: a learning experience which describes the background to my personal heuristic discovery & proof of this general 'interior angle sum' theorem.
c) A general formula for the interior angle sum of polygons is given at A general formula for the interior angle sum of polygons.
d) Read my 1999 Math in School article Stars: A second look for a short proof of this general formula, and for more examples, see Problem 15 on pp. 49-50 and the Solutions on pp. 135-136 of my book Some Adventures in Euclidean Geometry.
e) Abelson, H. & diSessa, A. (1983). Turtle Geometry: The computer as a medium for exploring mathematics. Cambridge, MA: The MIT Press.
f) De Villiers, M. (2020). The Value of using Signed Quantities in Geometry Learning & Teaching Mathematics, Dec 2020, No. 29.
Related Links
Back
to "Dynamic Geometry Sketches"
Back
to "Student Explorations"
Michael de Villiers, created 25 January 2011, adapted to WebSketchpad 12 August 2021; updated 27 June 2023