Diagonal Division Ratios in a Quadrilateral

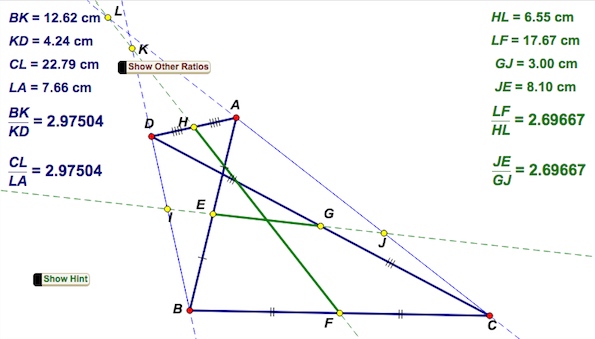
Given a quadrilateral ABCD, with E, F, G and H the respective midpoints of AB, BC, CD and DA. Label as I and J the respective intersections of EG with diagonals BD and AC, and K and L the respective intersections of HF with diagonals BD and AC.
1) Drag any of the red vertices A, B, C or D and carefully look at the displayed values.
2) What do you notice? Can you formulate a conjecture?

3) Can you explain why (prove that) your conjecture(s) above are true? Only if stuck, click on the provided Show Hint.

4) From the above result, can you give two more pairs of ratios that are equal? Check your answer by clicking on Show Other Ratios, and by further dragging.

Diagonal Ratios

Note: Observe by dragging that the result is also true if ABCD is concave as well as crossed as shown above.

Back to "Dynamic Geometry Sketches"

Back to "Student Explorations"

Michael de Villiers, created 24 October 2018.

Diagonal Division Ratios in a Quadrilateral

.sketch_canvas { border: medium solid lightgray; display: inline-block; }