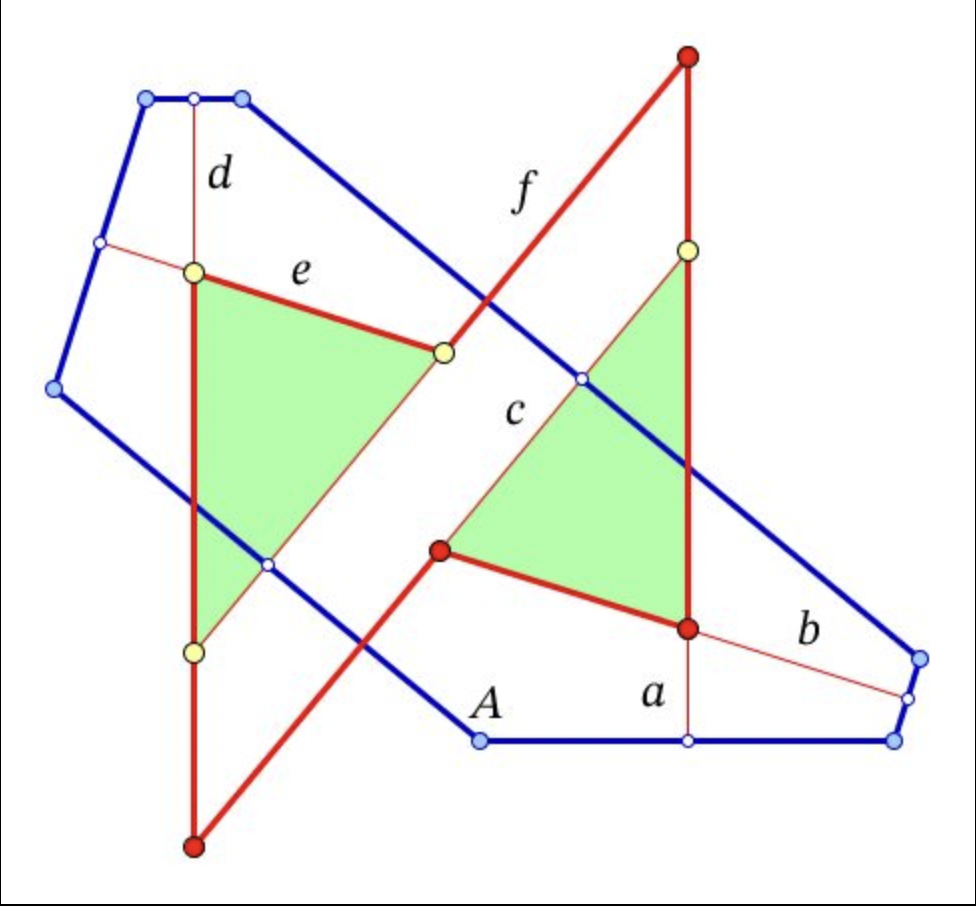
The following neat transformation proof by Vladimir Dubrovsky, Moscow, Russia, for the result was given in a post on 22 November 2021 at the Romantics of Geometry group on Facebook: here.

Proof: Denote by a,b,...,f the perpendicular bisectors in natural order, by A the common vertex of the sides corresponding to f and a, and by ∆1 and ∆2 the triangles formed by a,b,c and d,e,f resp. ∆1 is taken into ∆2 by a homothety H with some ratio k (because their corresponding sides are parallel). It suffices to prove that k= -1; then ∆1 and ∆2, and hence the hexagon in question, are symmetric about some center. Consider the compositions G1 and G2 of reflections in a, b, c and in d, e, f, resp. Each of them is a glide reflection; let m1, v1 and m2, v2 be their axes and translation vectors, then m2=H(m1), and so m1 ∥ m2, and v2=k∙v1. Therefore, T=G2◦G1 is a translation. On the other hand, T, the composition of all the 6 reflections in a, b, ..., fixes point A. So it is the zero translation. It follows that m1=m2 and v1=-v2, or k=-1, as required.
***********Back
to "Dynamic Geometry Sketches"
Back
to "Student Explorations"
Created by Michael de Villiers, 29 November 2021.