Eight Point Conic for Cyclic Quadrilateral

Problem: The following problem was posed by myself and Michael Fox in the Problem Corner of the Mathematical Gazette, Nov 2006: The diagonals of a cyclic quadrilateral ABCD meet at P. The feet of the perpendiculars from P to AB, BC, CD, DA are E, F, G, H. The lines EP, FP, GP, HP meet the opposite sides of ABCD at K, L, M, N. Prove that E, F, G, H, K, L, M, N lie on a conic.

Eight Point Conic for Cyclic Quadrilateral

Note: The result is also true if ABCD becomes a crossed quadrilateral, but the above dynamic sketch, due to certain construction limitations, is unfortunately not able to show it. However, as shown by the Cinderella sketch below, the result is also true for the crossed case.

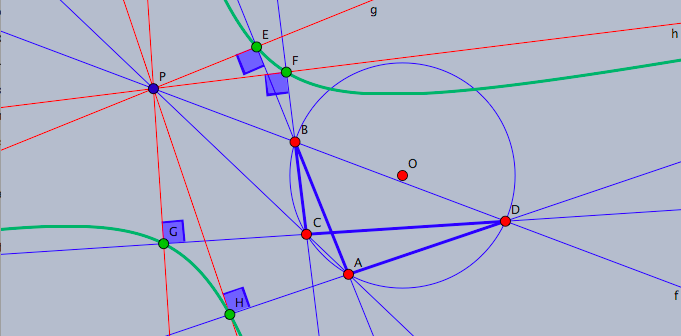
Download the dynamic geometry software Cinderella 2 for FREE from here, and use it (after unzipping) to view & manipulate the Cinderella Eight Point Conic sketch illustrating the above result.

Challenge: Can you explain why (prove that) the above result is true? Can you generalise further?

If stuck, go to Proof & Further Generalizations.