NOTE: Please WAIT while the applet below loads.
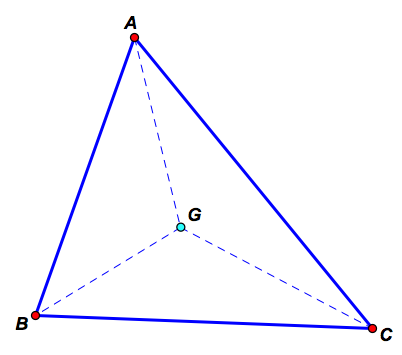
As is well known, the centroid G of a triangle ABC divides, or equi-partitions, the triangle into three triangles, AGB, BGC, and CGA, of equal area as shown below.

What about a quadrilateral? Can we find a similar point P for a quadrilateral ABCD that divides, or equi-partitions, it into four triangles, APB, BPC, CPD and DPA, of equal area?
1) Use the dynamic sketch below to explore the problem by dragging P to see if you can find such a position.
2) Change the shape of ABCD to see for what kind of quadrilateral(s) you can find a position for P that satifies the 'equi-partitioning' condition stated above.
Equi-partitioning Point of a Quadrilateral
Conjecture
3) What conjectures have you made? Can you explain why (prove) that they are true?
4) Check your conjectures, and your proofs, in this paper by Shan & Poobhal Pillay (2010) at: Equipartitioning and Balancing Points of Polygons.
5) Also visit this webpage, which relates to the results mentioned in 4) above: More Properties of a Bisect-diagonal Quadrilateral.
Back
to "Dynamic Geometry Sketches"
Back
to "Student Explorations"
Created by Michael de Villiers, 10 August 2020.