Extangential Quadrilateral

An extangential quadrilateral is a quadrilateral with an excircle as shown below. In other words, the extensions of all four of its sides are tangent to a circle exterior to the quadrilateral. Hence, the exterior angle bisectors at A, B and D are concurrent at the excentre.
An interesting property of the extangential quadrilateral is that it has two (distinct) sums of adjacent sides equal. For example, as illustrated in the sketch: a + b = c + d.
The extangential quadrilateral is a close relative of the tangential/circumscribed quadrilateral which has two sums of alternate (opposite) sides equal.

Web Sketchpad

Extangential Quadrilateral

Challenge
1) Can you prove that if a quadrilateral has an excircle that it has two (distinct) sums of adjacent sides equal?
2) Can you prove the converse, namely that if a quadrilateral has two (distinct) sums of adjacent sides equal then it has an excircle?
3) Apart from the 3 exterior angle bisectors at A, B and D concurrent at the excentre, there are 3 more angle bisectors concurrent at the excentre. Can you identify them?

Explore More
4) Can you drag the extangential quadrilateral into a concave or crossed shape?
5) Which quadrilaterals are special cases of an extangential quadrilateral? Explore by dragging or consider those that meet its definition.
An extangential quadrilateral has many properties, many of which have been extensively explored by Martin Josefsson (see references below). Here is an interesting angle property.
6) Click on the 'Show Angles1' button.
7) What do you notice? Check by dragging.
8) Challenge: Can you explain why (prove that) your observation in 7) is true?
Note: A proof of the property in 8) appears in Josefsson (2016).

Side-Angle Duality
Of further special interest is that according to the side-angle duality/analogy already observed by Coolidge in 1916, and also explored in De Villiers (1996) in relation to the classification of quadrilaterals, the extangential quadrilateral is the dual of the trapezium (trapezoid).
The side-angle duality is clearly apparent in that a trapezium has two (distinct) sums of adjacent angles equal (e.g. ∠A + ∠B = ∠C + ∠D) while an extangential quadrilateral has two (distinct) sums of adjacent sides equal (e.g. a + b = c + d).
Since a well-known theorem of a trapezium is the so-called Midpoint/Midsegment Theorem of a Trapezium (with the midsegment equal to half the sum of the two parallel sides), it seems natural to wonder if a similar relationship holds for some angles in an extangential quadrilateral.
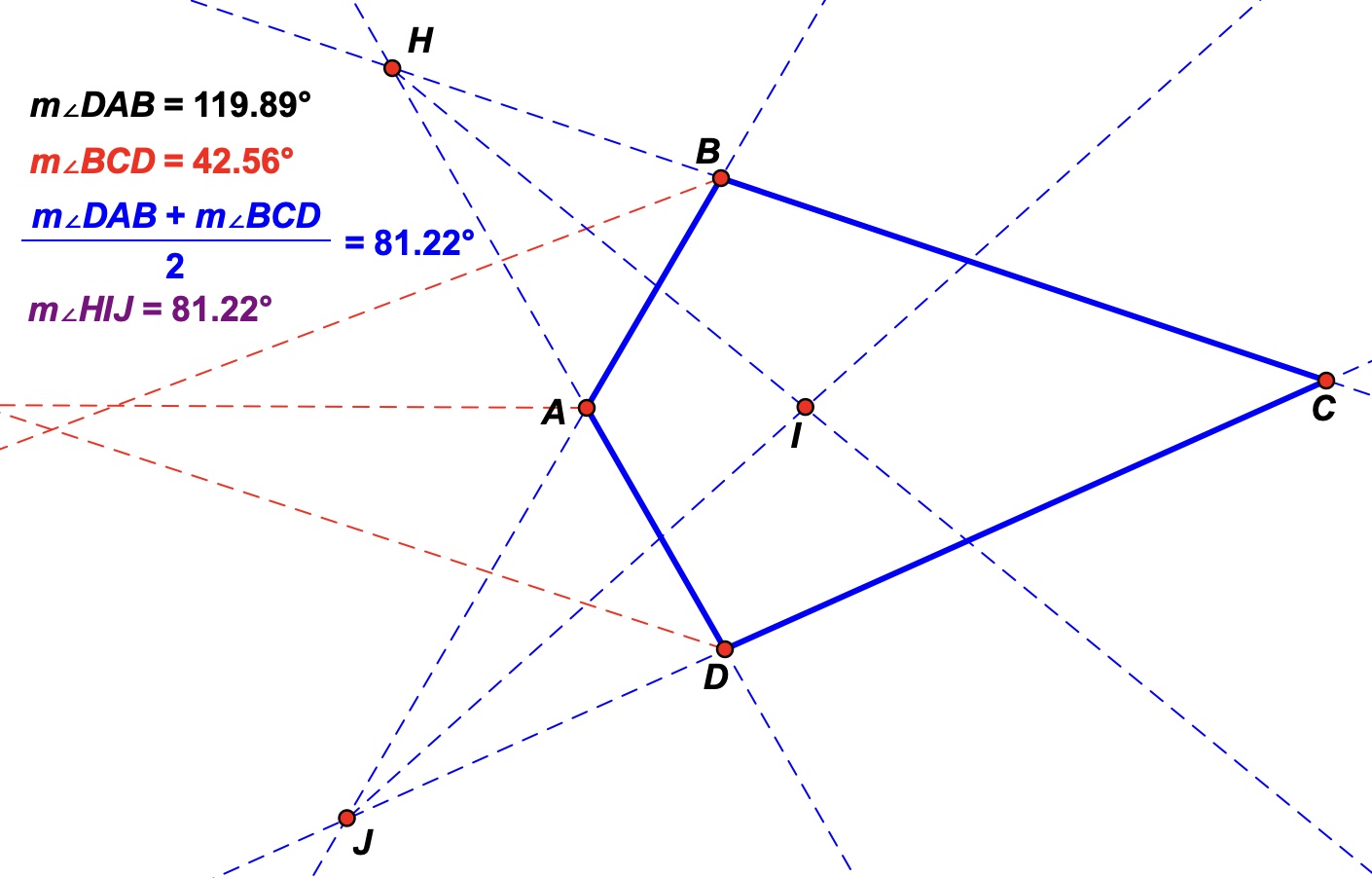
9) Click on the 'Show Angles2' button.
Here the angle bisectors of angles DHC and CJB have been constructed to meet at point I.
10) What do you notice about the relationship between ∠HIJ and ½(∠DAB + ∠BCD)? Check your observation by dragging.
11) Challenge: Can you explain why (prove that) your observation in 10) is true?
(Remark: This easy to prove 2nd angle property does not appear in the articles by Josefsson referenced below since it is NOT a sufficient condition for a quadrilateral to be an extangential quadrilateral, and is true for any complete quadrilateral as shown in the sketch below. For example, note that the angle bisectors of angles HAJ, HBJ and HDJ, shown in red, are not concurrent. Therefore the quadrilateral is not extangential.)

angle property of complete quadrilateral

Generalization
12) Can you generalize the concept of an extangential quadrilateral in a meaningful way to extangential pentagons, hexagons, etc.? Explore on your own.

Acknowledgement
I first learnt of this interesting quadrilateral from Martin Josefsson (Sweden) who attributes the first proof of this result in 1846 to the famous Swiss mathematician Jakob Steiner (1796-1863). Josefsson has done an extensive study of the properties of extangential as well as tangential quadrilaterals - see references below.
More recently, Humenberger (2023) identified 6 different possible cases of tangential and extangential quadrilaterals having incircles or excircles, including concave and crossed cases.

References
Coolidge, J.L. (1916). A Treatise on the Circle and the Sphere (pp 53-57). Bronx, NY: Chelsea Publishing Company.
De Villiers, M. (2009). Some Adventures in Euclidean Geometry (Free to download). Lulu Publishers.
Humenberger, H. (2023). Unusual Cyclic and Tangential Quadrilaterals – An Overview. Mathematics in School, May, pp. 26-32.
Josefsson, M. (2012). Similar Metric Characterizations of Tangential and Extangential Quadrilaterals. Forum Geometricorum, Vol 12, pp. 63-77.
Josefsson, M. (2016). More Characterizations of Extangential Quadrilaterals. International Journal of Geometry, Vol. 5, No. 2, 62-76.
Josefsson, M. & Dalcín, M. (2021). 100 Characterizations of Tangential Quadrilaterals. International Journal of Geometry, Vol. 10, No. 4, 32 - 62.

External Links
Ex-tangential quadrilateral (Wikipedia)
SA Mathematics Olympiad
Questions and worked solutions for past South African Mathematics Olympiad papers can be found at this link.
(Note, however, that prospective users will need to register and log in to be able to view past papers and solutions.)

***************

Free Download of Geometer's Sketchpad

***************

Back to "Dynamic Geometry Sketches"

Back to "Student Explorations"

Created by Michael de Villiers with WebSketchpad, 25 July 2020; updated 5 April 2025.