Since the Cinderella sketch above is based on Java, it is unfortunately not likely to run any more on newer computers & new browsers. However, here is a video clip illustrating the sketch:
(Click on the pic below to navigate to & activate the clip)
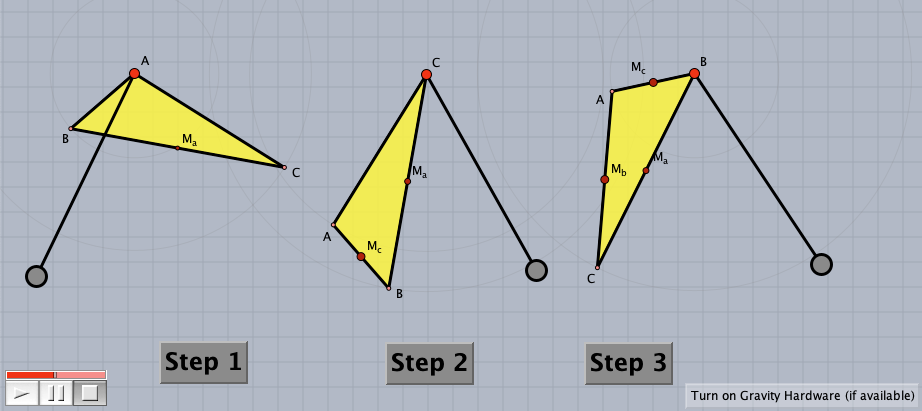
The Cinderella sketch above simulates how one can experimentally find the median of a carboard triangle by pinning it at one of its vertices, and letting it loose to swing freely, then the median (or 'balance line') will align with a vertical plumb line. By pinning the triangle at the other two vertices, the other two medians can be found, and the intersection of the three medians then gives us the centroid ('balancing point') of the whole triangle.
Instructions: Press the PLAY button on the bottom left to start.Then press in succession, the STEP 1, STEP 2 and STEP 3 buttons. After the triangle and plumb line has come to rest you can also drag the vertices of the triangle or the plumb line. Press the STOP button to reset.
Video Clip
Since the Cinderella sketch above is based on Java, it is unfortunately not likely to run any more on newer computers & new browsers. However, here is a video clip illustrating the sketch:
(Click on the pic below to navigate to & activate the clip)

A free classroom worksheet with guided activity & proof about the concurrency of the medians is available in my Rethinking Proof with Sketchpad book (pp. 51-56; 163-168 (teacher notes)), and information is provided inside at the beginning on where to download the accompanying Sketchpad sketches from.
Explore further how to experimentally find the centroid (balancing point) for a triangle with different weights at the vertices at Experimentally Finding the Centroid of a Triangle with Different Weights at the Vertices, and also how this is a physical representation of Ceva's theorem (1678).
Now explore further how to balance quadrilaterals interactively at Centroid of Cardboard Quadrilateral and Point Mass Centroid of Quadrilateral.
Watch NASA clip about locating centres of gravity of aircraft
Back to "Dynamic Geometry Sketches"
Back to "Student Explorations"
Created with Cinderella by Uli Kortenkamp & slightly modified by Michael de Villiers, March 2009; updated 15 March 2021; 16 March 2024.