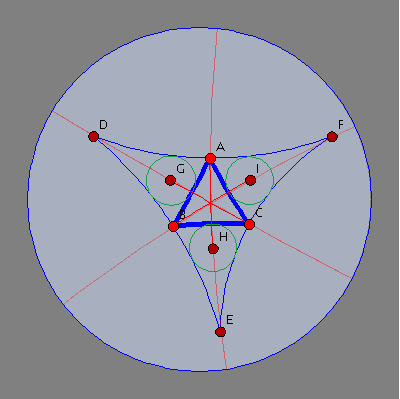
Consider the sketch below where D, E and F are the excentres of the hyperbolic triangle ABC on the Poincare' disk, and G, H and I are the respective incentres of ABD, BCE and CAF. Drag any of the vertices of the hyperbolic triangle to investigate whether AE, BF and CD are always concurrent. What do you notice? Can you prove (or refute) your observation?

Created by Michael de Villiers, 24 January 2011 with Cinderella. A free version of Cinderella 1.4 - the only dynamic geometry software that can also do elliptic (spherical) geometry and hyperbolic geometry - can be downloaded from Download Cinderella 1.4.