A circle is a two dimensional object that has constant width; its height remains constant regardless of the orientation. (In other words, any two parallel lines, each tangent to the circle is the same distance apart). Can you construct another two-dimensional figure that has constant width, but is not a circle? Perhaps surprisingly, it is possible!
The Reuleaux triangle is probably the best known curve of 'constant width', and is constructed by drawing circular arcs from each vertex of an equilateral triangle between the other two vertices. See for example, Reuleaux triangle
Curves of Constant Width have several useful applications as shown in Constant Width Applications
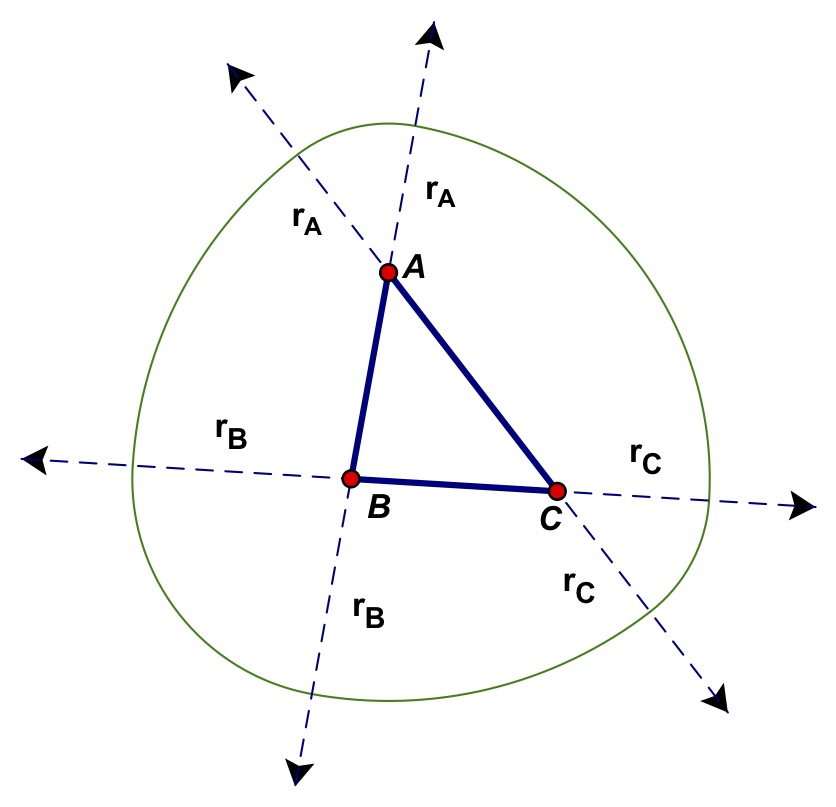
My friend and colleague from the SA Mathematics Olympiad for many years, James Ridley, recently (April 2010) wondered whether one could generalize the Reuleaux triangle to any scalene triangle. To his surprise (and mine) he found it was possible! Read his short paper at Reuleaux triangle Generalization which includes a link to a short video clip showing a dynamic Sketchpad construction of the generalization.

Unfortunately as often happens, the result is not new, but was nonetheless an interesting exercise. For more information on Curves of Constant Width (including this generalization) go to Curves of Constant Width and scroll the page about half-way down.
Michael de Villiers, 11 August 2010.