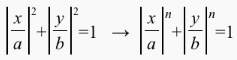
Though the Danish poet and scientist Piet Hein (1905–1996) is often credited with the discovery of the super-ellipse, it was the geometer Gabriel Lamé (1818) who first generalized the concept of an ellipse to a super-ellipse by generalizing the exponents of the standard equation of an ellipse as shown below:
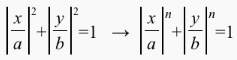
This super-ellipse formula can be converted to the following equivalent, polar coordinate form by substituting x = r.cos θ and y = r.sin θ into the above equation and solving for r to obtain:
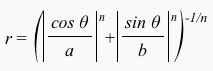
More recently, the Belgian Botanist, Johan Gielis (1996, 2003) from Antwerpen generalized the polar coordinate version further as follows by considering possibly different values of the exponents and also including a factor m/4 to divide the polar coordinate plane into m sectors:
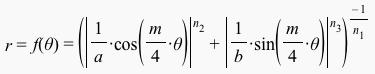
References
Gielis, J. (1996) Wiskundige supervormen bij bamboes. Newsletter of the Belgian Bamboo Society 13 (December 2, 1996), 20-26.
Gielis J. (2003) A generic geometric transformation that unifies a large range of natural and abstract shapes. American Journal of Botany 90(3), Invited Special Paper, 333-338.
Lamé, G. (1818) Examen de differentes méthodes employées pour résoudre les problèmes de géometrie. M. V. Courcier imprimeur Libraire. (New Edition 2008 from Editions Gabay).
Note: In the dynamic JavaSketchpad sketch below, the above formula is represented. Drag the red points m, n1, n2, n3, a or b to explore the huge and intriguing variety of symmetric figures that are produced with the Gielis super shape formula. (Unfortunately the slider values in the JavaSketchpad sketch change discreetly so only approximate values for whole numbers can sometimes be obtained).
The Gielis Super Shape Formula
A fascinating aspect of the Gielis Super Shape formula is that it can be used to model the shape of numerous natural objects from plants and flowers to snowflakes and crystals. For example, the shape shown above, produced by the parameter values (6, 100, 38, 38, 0.5, 1) - in the order (m, n1, n2, n3, a, b) - resembles that of the snowflake shown in the first picture below1 (and by making a = b, we obtain a regular hexagon). Try the parameter values (6, 100, 100, 100, 1, 1) and you should get a shape similar to that of the second snowflake below. The parameter values (4, 10, 19, 19, 0.9, 0.9) and (5, 2, 9, 9, 1, 1) produce shapes approximately corresponding to a cross-section of a certain type of cactus and that of a starfish, respectively shown by the 3rd and 4th figures below. (For the starfish shape, you can resize the figure by dragging the yellow point on the x-axis.)




FootNote 1: A snowflake hexagon like the first one above can be called a semi-regular angle-gon since all the angles are equal and the two pairs of alternate sides are equal. Read more about semi-regular polygons at Generalizations of rectangles and rhombi.
Use the above dynamic sketch to further explore the effect of the parametersor use the animation buttons. Many other examples of shapes produced by the Gielis formula can be found in the online encyclopedia, Wikipedia, at Super Formula.
The parameter m basically determines the number of 'sectors', 'bulges', 'hollows' or 'corners' of the shape. When m = 0, the shape is a circle, but with m = 4, depending on the value of the other parameters, we can get a square with four vertices, or a shape like the cactus cross section with four 'corners' and four 'hollows', or a standard ellipse (which has two narrow 'bulges' and two wide ones). If n1 > n2 = n3 the sides can tend to straight lines and with appropriate values, regular polygons can be produced. The parameters a and b determine the lengths of the major axes and therefore the size of the shape. With higher even values of m, different values of a and b, will produce alternate sides of different length.
The Gielis super shape formula can be generalized to 3D in at least two different ways, for example, by rotating the 2D version around one of the axis, or by using polar coordinates in 3D. The 2D formula itself can obviously be further generalized by considering different parameters for m in the two parts of the formula it occurs. Though the creation of closed figures are important if one wants to model closed shapes such as flowers or snowflakes, mathematically nothing prevents us to modify the Gielis super shape formula by instead of adding the two absolute values, we could simply subtract the second one from the first to produce a Super Hyperbola formula as shown below:
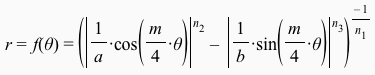
In the Link in the dynamic WebSketchpad sketch above, the Super Hyperbola formula is represented. Have FUN dragging the red points m, n1, n2, n3, a or b to explore the huge and intriguing variety of symmetric and other figures that are produced with this formula! Which set(s) of values for the parameters would produce regular hyperbola?
Note: The slider values in the JavaSketchpad sketch unfortunately change discreetly; so only approximate values for whole numbers can mostly be obtained. Therefore, because of these approximations, each hyperbolic branch of the Java sketch for (5, 2, 2, 2, 1, 1) appears to 'split' into two as it goes off to infinity. Also be aware, that the JavaSketchpad sketch, for some values of the parameters, does not always correctly display asymptotes and branches going off to infinity. For more accurate explorations, it is better to use either Sketchpad or some other similar graphing software. Accurate Sketchpad 5 sketches for both the Gielis formula and the Super Hyperbola formula are available for downloading at Gielis Super Shape Formula and Super Hyperbola.
Created by Michael de Villiers, 19 June 2011; updated 3 June 2019.