Toshio Seimiya Theorem: A Hexagon Concurrency result

The surprising theorem below by Toshio Seimiya from Japan was communicated to me in July 2018 by my friend and colleague from Poland, Waldemar Pompe:
"In a plane hexagon ABCDEF, the lines joining the midpoints of the opposite sides are concurrent, if and only if, triangles ACE and BDF have equal areas."

Drag any of the red vertices A, B, C, D, E or X to dynamically change the configuration.

This theorem is a generalization of the special case when ABCDEF is a hexagon with opposite sides parallel (but not necessarily equal) - see Parallel-Hexagon Concurrency Theorem.

Note: In certain crossed configurations, the above sketch will unfortunately not correctly show the concurrency of the lines due to a software design decision by the GSP computer programmers regarding the relative movement of points on a line when they are supposed to cross over and interchange. For the general case, one also needs to assume signed areas, which the software also doesn't handle.

Challenge:
Although the Seimiya Theorem lends itself most readily to attack by vector methods or complex algebra, the real challenge is to find a purely geometric proof. Can you find such a proof?

Proof:
Here's a nice, elegant proof with vectors and coordinates by my long-time friend and colleague, Michael Fox - click here to view or download.

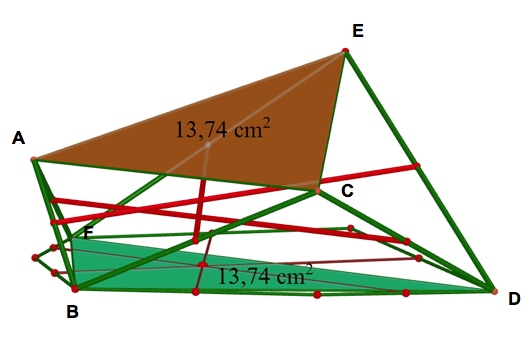
Generalization to 3D:
Interestingly, and perhaps even more surprisingly, is that though triangles ACE and BDF having equal areas is a sufficient condition for the Seimiya theorem in the plane, this is not the case in 3D. As shown by the counter-example below, using Cabri 3D, and produced by my friend and colleague from Germany, Heinz Schumann, this is not true for a spatial 3D hexagon. As shown below, triangles ACE and BDF having equal areas in 3D space, do not necessarily imply that the lines connecting the midpoints of opposite sides are concurrent.

For a spatial '3D-parallelo-hexagon', the forward implication of the Seimiya theorem for a 3D-spatial hexagon follows directly from its point symmetry.
The concept of a 3D-parallelo-hexagon was discussed in a paper by Heinz Schumann & myself in the July 2018 issue of 'The Mathematical Gazette', and is available to download at: A surprising 3D result involving a hexagon. A 3D-parallelo-hexagon is also formed by the centroids of the triangles subdividing any 3D-hexagon as shown at: Triangle Centroids of a Hexagon form a Parallelo-Hexagon.

Back to "Dynamic Geometry Sketches"

Back to "Student Explorations"

Michael de Villiers, created 3 January 2019, updated 24 March 2019.