Quadrilateral Balancing Theorem: Another 'Van Aubel-like' theorem (2007)
Published Paper
For a proof of the above, read my 2007/2008 article in the Mathematical Gazette: A Question of Balance: An Application of Centroids.
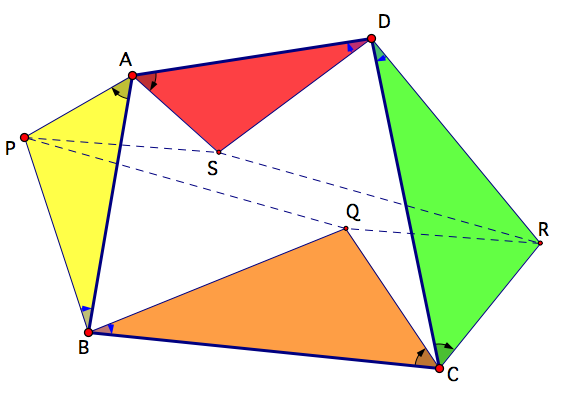
Similar Triangles on Sides of Quadrilateral Theorem
Given a quadrilateral ABCD with similar triangles PBA, QBC, RDC and SDA constructed on the sides so that say the first and third are exterior to the quadrilateral, while the second and the fourth are interior to the quadrilateral, then quadrilateral PQRS is a parallelogram.
Important: To view & manipulate the dynamic version of this result, navigate to it by clicking on the 'Link to Similar Triangles' button in the ABOVE dynamic sketch; the picture below is static.
Directly Similar Triangles on Sides of Quadrilateral Theorem (1994)
1) A proof of the above result appears on pp. 145-148 of the (1994/2009) edition of my book Some Adventures in Euclidean Geometry as well as in my paper The Role of Proof in Investigative, Computer-based Geometry: Some personal reflections, a chapter in the 1997 MAA book, Geometry Turned On!, edited by Doris Schattschneider & Jim King.
2) However, this result has appeared earlier in Finney (1970) who references Van Aubel (1881) for the original result.
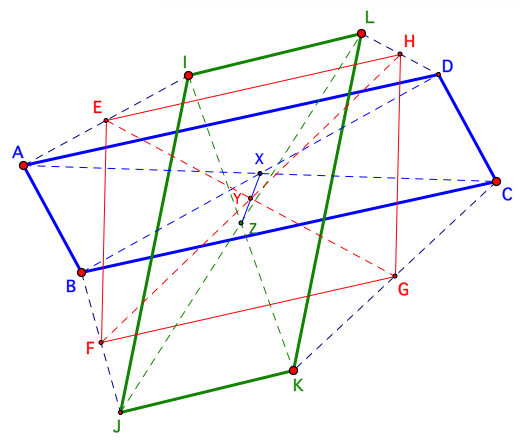
Lemma: A Trio of Parallelograms
Given two parallelograms ABCD and IJKL, the midpoints E, F, G, H of the segments AI, BJ, CK, DL form another parallelogram. More-over, the centre Y of EFGH is the midpoint of XZ where X and Z are respective centres of ABCD and IJKL. (The diagram shows a case with the parallelograms both labelled anticlockwise, but both lemma and proof work equally well in all cases.)
Important: To view & manipulate the dynamic version of this result, navigate to it by clicking on the 'Link to Lemma Parallelograms' button in the ABOVE dynamic sketch; the picture below is static.
Lemma: A Trio of Parallelograms (2007)
The lemma above, together with the Directly Similar Triangles Theorem, was used to prove the Quadrilateral Balancing Theorem in my 2007/2008 article in the Mathematical Gazette: A Question of Balance: An Application of Centroids.
References
De Villiers, M. (1994/2009). Some Adventures in Euclidean Geometry (free download), Lulu Publishers.
De Villiers, M. (1997). The Role of Proof in Investigative, Computer-based Geometry: Some personal reflections, in D. Schattschneider & J. King (Editors), Geometry Turned On!, MAA.
De Villiers, M. (2007/2008). A Question of Balance: An Application of Centroids, Mathematical Gazette, Nov 2007, pp. 525-528; March 2008, pp. 167-169.
Finney, R. L. (1970). Dynamic Proofs of Euclidean Theorems, Math Magazine, 43, pp. 177-185.
Van Aubel, M.H. (1881). Question 56, Mathesis, no. 1, p. 167.
Related Links
Van Aubel's theorem and some Generalizations
An associated result of the Van Aubel configuration and some generalizations
Van Aubel Centroid & its Generalization
Triangle Centroids of a Hexagon form a Parallelo-Hexagon: A generalization of Varignon's Theorem
Centroid Properties of a Bisect-diagonal Quadrilateral
Finsler-Hadwiger Theorem plus Gamow-Bottema's Invariant Point
A Fundamental Theorem of Similarity
Napoleon's Theorem: Generalizations & Converses
Some Variations of Vecten configurations
Experimentally Finding the Medians and Centroid of a Triangle
Experimentally Finding the Centroid of a Triangle with Different Weights at the Vertices
Two different centroids (balancing points) of a quadrilateral
A generalization of a Parallelogram Theorem to Parallelo-hexagons, Hexagons and 2n-gons in general
External Related Links
Similar Triangles on Sides of a Quadrilateral (Cut The Knot)
Squares on Sides of a Quadrilateral (Cut The Knot)
Van Aubel's theorem (Wikipedia)
Balanced areas in quadrilaterals - on the way to Anne's Theorem
**************
Free Download of Geometer's Sketchpad
Back to "Dynamic Geometry Sketches"
Back to "Student Explorations"
Created 2013 by Michael de Villiers. Most recent updates, 16 March 2020; 19 February 2022; 25 Jan 2025.