Van Aubel's Theorem and some Generalizations

Henri van Aubel (1830-1906)

Van Aubel's theorem: If squares are constructed on the sides of any quadrilateral, then the segments connecting the centres of the squares on opposite sides are perpendicular and of equal length.

NOTE: Please WAIT while the applet below loads.

Van Aubel's Theorem

Historical Note: Van Aubel taught pre-university mathematics at the Koninklijk Atheneum in Antwerpen ( Belgium) and it seems that his theorem first appeared in Nouvelles Corresp. Mathematique 4 (1878), pp 40-44.

A Generalization of Van Aubel's Theorem to Similar Rectangles (1994 or earlier)

If similar rectangles with centres E, F, G and H are erected externally on the sides of quadrilateral ABCD as shown, then ∠FOG = 90^o and EG/FH = XA/AB. Further, if J, K, L and M are the midpoints of the dashed segments shown, then KM = JL, and the angle of JL and KM equals the angle of the diagonals of the rectangles. (Also note that lines EG, FH, KM and JL are concurrent in O, and that the line FH bisects ∠KOL, etc.)

Important: To view & manipulate the dynamic version of this result, navigate to it using the appropriate button in the ABOVE dynamic sketch; the picture below is static.

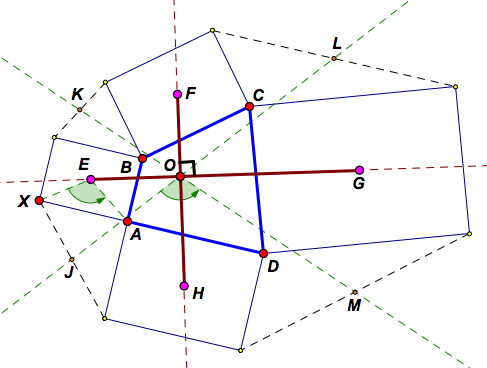
A Generalization of Van Aubel's Theorem to Similar Rectangles

A Generalization of Van Aubel's Theorem to Similar Rhombi (1994)

If similar rhombi with centres E, F, G and H are erected externally on the sides of quadrilateral ABCD as shown, then EG = FH and ∠FWG = ∠ABY. Further, if J, K, L and M are the midpoints of the dashed segments shown, then KM/JL = YA/XB, and the angle of JL and KM equals the angle of the diagonals of the rhombi (= 90^o).

Important: To view & manipulate the dynamic version of this result, navigate to it using the appropriate button in the ABOVE dynamic sketch; the picture below is static.

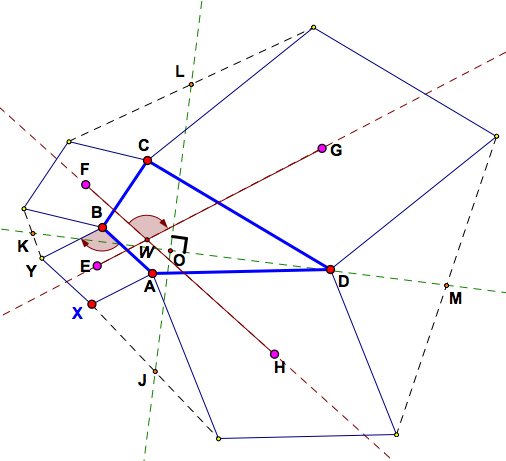
A Generalization of Van Aubel's Theorem to Similar Rhombi (1994)

A Generalization of Van Aubel's Theorem to Similar Parallelograms (Hessel Pot, 1997)

If similar parallelograms with centres E, F, G and H are erected externally on the sides of quadrilateral ABCD as shown, then FH/EG = XY/YB , and the angle of EG and FH equals the angle of the sides of the parallelograms. Further, if J, K, L and M are the midpoints of the dashed segments shown, then KM/JL = YA/XB, and the angle of JL and KM equals the angle of the diagonals of the parallelograms.

Important: To view & manipulate the dynamic version of this result, navigate to it using the appropriate button in the ABOVE dynamic sketch; the picture below is static.

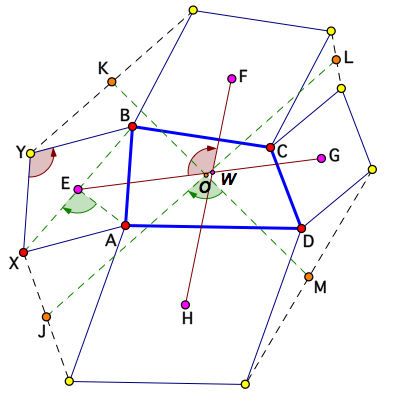
A Generalization of Van Aubel's Theorem to Similar Parallelograms (1997)

Associated Results of Van Aubel & their Generalization
For an interesting associated result of Van Aubel's theorem, click on An associated result of the Van Aubel configuration and some generalizations to open & view in a new window.
For a result involving the vertex centroid of a Van Aubel configuration, click on The Vertex Centroid of a Van Aubel Result involving Similar Quadrilaterals and its Further Generalization to open & view in a new window.

Some Corollaries of Van Aubel Generalizations
For some interesting corollaries, click on Some Corollaries of Van Aubel Generalizations to open them in a new window.

Twin circles of the Van Aubel Similar Parallelogram Generalization
Click on Twin circles of a Van Aubel Generalization to open them in a new window.

Some Articles
1) Read my chapter in Schattschneider, D. & King, J. (1997). Geometry Turned On! Washington: MAA, pp. 15-24. The Role of Proof in Investigative, Computer-based Geometry: Some Personal Reflections (1997).
2) Read my 1998 article in the "Mathematical Gazette", also about similar rectangles or similar rhombi on the sides of a quadrilateral, but different proofs to those in the chapter above Dual Generalizations of Van Aubel's Theorem.
3) My "Mathematics Magazine" article in 2000 Generalizing Van Aubel using Duality, which mentions, without proof, the further generalization to similar parallelograms, and even further generalizations due to Chris Fisher.
4) John Silvester's excellent 2006 "Mathematical Gazette" article gives different proofs and some further Extensions of a theorem of Van Aubel.
5) The website of Dick Klingens (in Dutch) provides proofs, and a related result for congruent rectangles on the opposite sides of a cyclic quadrilateral with interactive Cabri applets and proofs. De Stelling van Van Aubel en algemenisering daarvan.
6) For another 'Van Aubel-like' theorem discovered in 2007 with directly similar quadrilaterals on the sides of a quadrilateral and their centroids go to Quadrilateral Balancing Theorem.
7) In 2011, Dick Klingens posed an interesting Problem of two intersecting circles or two adjacent isosceles triangles, which turns out to be a special case of the 'similar rectangles' generalization of Van Aubel.
8) Read Yutaka Nishiyama's paper in the 2011 issue of the International Journal of Pure and Applied Mathematics at: The beautiful geometric theorem of Van Aubel.
9) Victor Oxman and Moshe Stupel provide Elegant special cases of Van Aubel’s theorem in the Math Gazette, July 2015.
10) Dào Thanh Oai on p. 19 of his 2016 paper Generalizations of some famous classical Euclidean geometry theorems in the International Journal of Computer Discovered Mathematics gives a perpendicularity lines Van Aubel generalization, distinctly different from the similar rectangles generalization given in De Villiers (1998) and Silvester (2006).
11) Dasari Naga and Vijay Krishna (2018) explore and prove several less-known properties in A note on special cases of Van Aubel’s theorem, International Journal of Advances in Applied Mathematics and Mechanics, 5(4), 30 – 51.
12) In 2019, Dario Pellegrinetti found an intriguing 6-point circle in relation to the basic Van Aubel configuration of squares constructed on the sides of a quadrilateral. Read his paper at: The Six-Point Circle for the Quadrangle.
13) Read An extension of the six-point circle theorem for a generalised Van Aubel configuration by Dario Pellegrinetti & myself in The Mathematical Gazette, 106(567), November 2022, pp. 400-407.
14) Read my 2023 paper in the Int. Journal of Math Ed in Sci & Technol.at: An associated result of the Van Aubel configuration and its generalization.

Historical note: Using dynamic geometry, I first discovered and then proved the similar rectangles and rhombi generalizations of Van Aubel in the early 1990's. Subsequently I published it in the 1st draft in 1994 of my "Some Adventures in Euclidean Geometry" book as well as in a 1997 MAA book "Geometry Turned On!" and with different proofs in a 1998 paper in the Mathematical Gazette. In subsequent communication with Hessel Pot from Woerden in the Netherlands in 1997, he mentioned that he had seen the similar rectangles generalization before, but not the similar rhombi one. He then also pointed out the neat further generalization to similar parallelograms on the sides.