(This page generalizes a problem posed at Dirk Laurie Tribute Problem.)
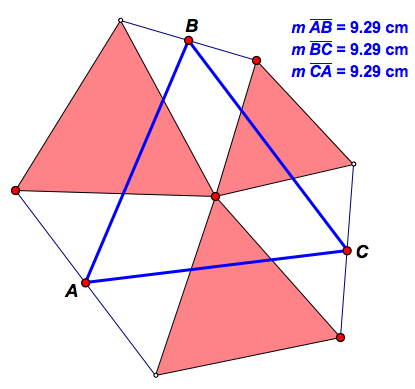
Generalization 1
The three equilateral triangles don't need to be of equal size as shown below. In other words, the outer vertices don't have to be cyclic.

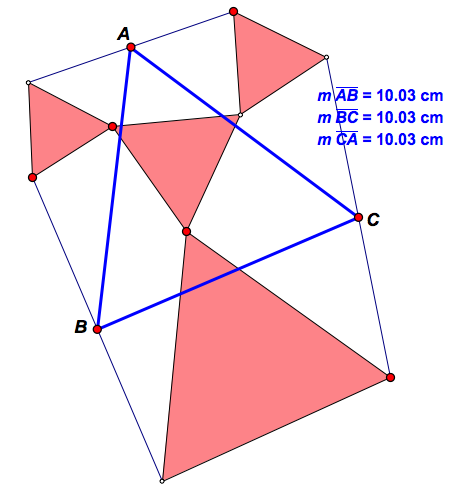
Generalization 2
The result can even be further generalized to four attached equilateral triangles as shown below.
Here is a nice animated dynamic sketch displaying the second generalization.
Challenge
1) Can you prove these generalizations purely geometrically?
2) Can you think of other possible generalizations or variations? Explore using dynamic geometry!
Hint: Try using spiral similarities (a combination of rotations and dilations) to prove the above. Or compare your proof for Generalization 2 to this proof by Mechri Tayyeb using complex numbers.
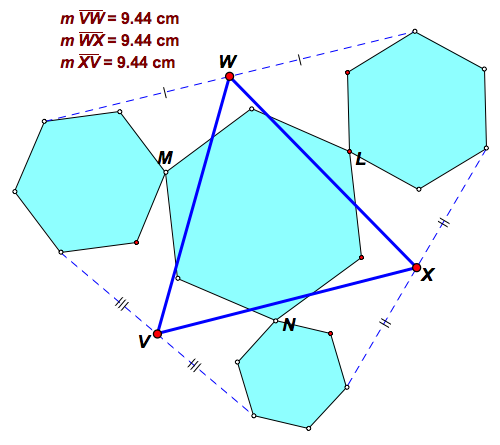
Here's a simple variation of Generalization 2 above using regular hexagons instead of equilateral triangles ...
Comment
The first generalization above has been called the Asymmetric Propeller theorem by Martin Gardner (1999) and can be seen to be equivalent to Napoleon's Theorem. Apparently the result is originally due to the nineteenth-century British mathematicians William Kingdom Clifford and Arthur Cayley. In 1973 Leon Bankoff, Paul Erdös and Murray Klamkin generalized the result further to the second generalization, as well as some further generalizations involving similar triangles. For more information go to: A Case of Similarity.
Some Related Links
Dirk Laurie Tribute Problem
Napoleon's Theorem
Napoleon's Theorem (a Rethinking Proof learning activity)
Some Triangle Generalizations of Napoleon's Theorem
Weighted Airport Problem
Related Variations & Generalizations of Napoleon's Theorem
Jha and Savarn’s generalisation of Napoleon’s theorem
The 120o Rhombus (or Conjoined Twin Equilateral Triangles) Theorem
Dao Than Oai’s generalization of Napoleon’s theorem
Some Napoleon Converses
Pompe's Hexagon Theorem
A variation of Miquel's theorem and its generalization
Some Variations of Vecten configurations
Some Circle Concurrency Theorems
Attached Regular Pentagons form Congruent Equilateral Triangles
Over and over: two geometric iterations with triangles
Another concurrency related to the Fermat point of a triangle plus related results
Quadrilateral Similar Triangles Collinearity
Some External Links
Asymmetric Propeller
A Case of Similarity
********************************
Back to "Dynamic Geometry Sketches"
Back to "Student Explorations"
Created 6 April 2020 by Michael de Villiers; updated 24 July 2020; 18 July 2025.