

Construction: A halfcircle on AB is constructed to pass through C,
as well as halfcircles on BC and AC as shown. The orange
'crescent moons' on BC and AC are called LUNES.
Investigate: Drag A, B or C. What do you notice about the sum of the areas of the lunes in relation to the area of △ABC? Make a conjecture.
(Note: The Greek mathematician, Hippocrates of Chios, is not to be confused with the different Greek physician of the Hippocratic oath in medicine.)
The theorem of Hippocrates (470 – c. 410 BC)
Challenge: Can you explain why (prove) your conjecture above is true?
Further Extension & Variation
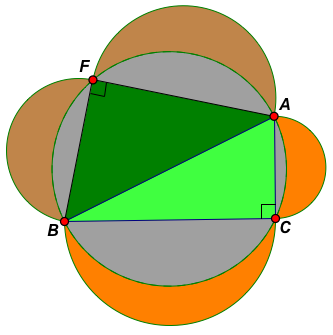
1) Click on the 'Link' button in the above sketch to navigate to a dynamic sketch that shows that Hippocrates' Theorem generalizes to a 'right quadrilateral' (more appropriately called a 'right Pythagorean quadrilateral' - see further on), namely, a quadrilateral with a pair of opposite right angles as shown in the first figure below. Here the sum of the lunes on the sides is equal to the area of the right Pythagorean quadrilateral1.
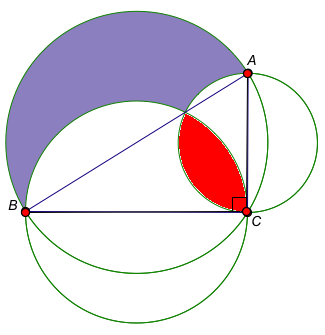
2) The second (static) figure below shows a variation of the theorem and in this case, the lilac (purplish-grey) region minus the red region is equal to the area of triangle ABC. Can you explain why (prove) this is true?
3) Explore further possible generalizations or variations on your own.
 ......
...... 
Notes
1) The term 'right quadrilateral' was originally used in my 1994/2009 book Some Adventures in Euclidean Geometry, pp. 73-74 for a quadrilateral with a pair of opposite right angles.
2) More recently, Martin Josefsson called this quadrilateral a 'right Pythagorean quadrilateral' in his highly recommended paper Properties of Pythagorean quadrilaterals in The Mathematical Gazette, 100(548), (July 2016), pp. 213-224.
3) Hippocrates' Theorem or variations of it appears on and off in Mathematics Competitions around the world. For example, see Q10 of the 2009 Second Round of the South African Mathematics Olympiad. The theorem also appeared in the Daily Problem, AMESA Congress, June 2009 and was used by Phadiela Cooper from COSAT to investigate the collaborative problem solving of children in small groups - the topic of her plenary at the AMESA Congress, University of the Western Cape, 24-28 June 2013.
Sketchpad sketches
Download and unzip Sketchpad sketches (221 kb) for Version 4 and Version 5 at: "GSP Sketches".
Back
to "Dynamic Geometry Sketches"
Back
to "Student Explorations"
By Michael de Villiers. Created, 31 July 2013; updated 23 June 2022.