Number Patterns: What numbers come next?

A typical question in many textbooks, tests, exams, quizzes, and even IQ tests, is the following: Write down the next three terms in the following sequence: 2; 6; 12; ...

 

What number comes next?

Since there is a difference of 4 between the first two numbers and a difference of 6 between the next two numbers, it may seem 'reasonable' that one may 'guess' that the next differences will be 8, 10 and 12, giving the next three numbers in the sequence as 20; 30; 42; ... However, if you thought the only correct answer is 20; 30; 42; ... then you were WRONG as there are INFINITELY many other possibilities!

For example, a cubic function (p - 20)x³/6 + (21 - p)x² + (11p - 214)x/6 + 20 - p with p a variable, can be drawn exactly through the first 3 points (indicated by points A, B and C in the graph above), but subsequent values of the function can assume any value as p is changed. Drag point P to change the graph and its function values.
(Note: The values of p in the slider above have, only for the sake of convenience, been restricted to integer values).

Explore more
1) Drag p until it equals 20 or 21. What do you notice?
2) What happens if p > 20? What happens if p becomes negative? Drag the point P far to the left until that happens.
3) Can you explain your observations above?

Generally, give a finite sequence of n numbers, infinitely many polynomials of order n or higher can be drawn through the n points. It is therefore complete mathematical NONSENSE in a test or exam to ask what the next terms are - unless a SPECIFIC CONTEXT (e.g. a figural pattern or some real world context) is also given that uniquely determines the pattern.

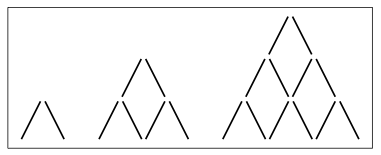
For example, Duncan Samson in his paper "The Heuristic Beauty of Figural Patterns" in Learning and Teaching Mathematics, no. 12, 2012, pp. 36-38, gives the following figural pattern for the number pattern at the start that uniquely determines it as 2; 6; 12; 20; 30; 42; ...

Similarly, even though the original Rabbit problem formulated by Fibonacci is not a genuinely real world problem, it nonetheless uniquely determines the number pattern 1; 1; 2; 3; 5; ... Without the context, however, the first 5 Fibonacci numbers can be modelled exactly by infinitely many quintic or higher order polynomials; let alone infinitely many other types of functions.

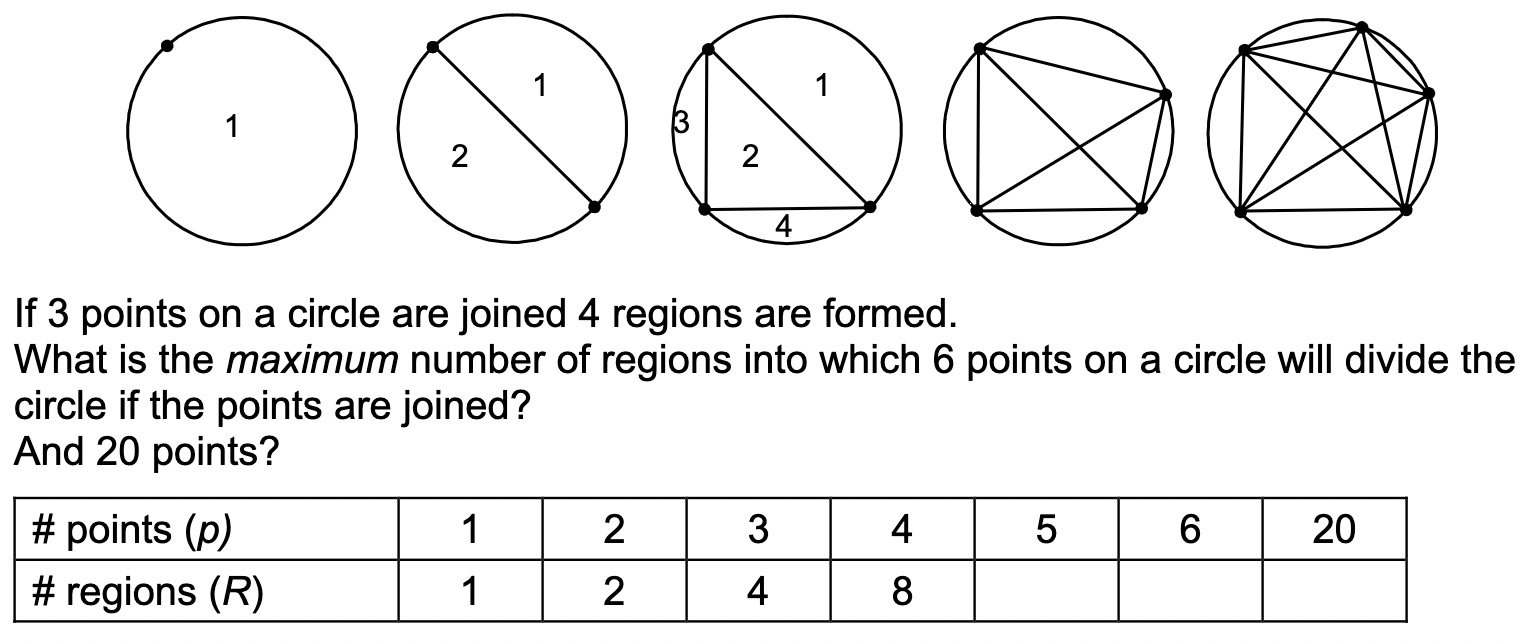
Lastly, students need to be constantly reminded that an inductive pattern, unless one has a formal, structural proof for why it works, may break down as in the well-known example given below: