Parallel-Hexagon Concurrency Theorem

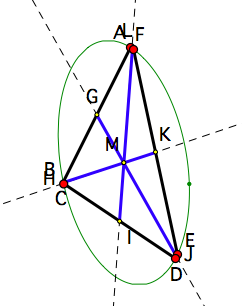
Theorem
If the midpoints of the opposite sides of a parallel-hexagon (a hexagon with opposite sides parallel - De Villiers (1994/2009)) are connected, then the three lines are concurrent at the centre of the conic circumscribed around the original hexagon.
(It seems appropriate to call the lines connecting the midpoints of opposite sides of the hexagon, midlines).
De Villiers, M. (1994/2009). Some Adventures in Euclidean Geometry. Morrisville, NC: Lulu Publishers.

 

Parallel-Hexagon Concurrency Theorem

Investigate
1) Drag A, B, C, D or E - also check when ABCDEF becomes a crossed hexagon.

Challenge
2) Can you explain why (prove that) the above result is true?

Special Case
3) Drag the vertices in pairs so that B and C, D and E, and A and F coincide, so that ABCDEF becomes a triangle (a degenerate hexagon). As shown below, this shows that the concurrency of the medians of a triangle is merely a special case of this more general theorem.

Published Paper
4) Download an article of mine from the Mathematical Gazette (2006) for a proof of the result above from More on Hexagons with Opposite Sides Parallel.

Further Generalization
5) Can you generalize even further to a more general hexagon? In this regard, have a look at: Toshio Seimiya Theorem: A Hexagon Concurrency result.

Related Paper
6) Bradley, C.J. (2006). Hexagons with Opposite Sides Parallel. The Mathematical Gazette, Vol. 90, No. 517 (Mar.), pp. 57-67.

Applications
7) Note that this theorem also applies to Thomson's crossed hexagon that appears in the Triangle Variation at Area ratios of some polygons inscribed in quadrilaterals and triangles.
8) Conway's hexagon and the more general side-divider hexagon which appears at Conway's Circle Theorem as special case of Side Divider Theorem is also a parallel-hexagon and the theorem above trivially applies to it. Note that in this case the circumscribing conic is a circle.

Related Links
Toshio Seimiya Theorem: A Hexagon Concurrency result
A theorem involving the perpendicular bisectors of a hexagon with opposite sides parallel
Conway's Circle Theorem as special case of Side Divider Theorem
Area ratios of some polygons inscribed in quadrilaterals and triangles
A side trisection triangle concurrency
A generalization of a Parallelogram Theorem to Parallelo-hexagons, Hexagons and 2n-gons in general
A 1999 British Mathematics Olympiad Problem and its dual
Easy Hexagon Explorations