Klingens' theorem of two intersecting circles or two adjacent isosceles triangles
(An application of a generalization of Van Aubel's Theorem)

In memoriam: A tribute to Dick Klingens (7 Mei 1945 - 24 Mei 2021)

The following intriguing problem was circulated by Dick Klingens at the annual meeting of the Nederlandse Vereniging van Wiskundeleraren (NVvW) in November 2011:
Formulation 1: Two circles K₁ and K₂ intersect each other in B and Q. A line through Q cuts K₁ in point A and K₂ in point C. The points E and F are the respective midpoints of the arcs BA and BC that do not contain Q. If M is the midpoint of AC, prove that ∠EMF = 90^o

Widgets

Dick Klingens' Problem

A different, but equivalent formulation of the same problem is the following:
Formuluation 2: Given two isosceles triangles ABC and BDE with respective bases AB and BD lying in a straight line (and on the same side of the line), and BC is perpendicular to BE. If M is the midpoint of AD, prove that ∠CME = 90^o.

Important: To view & manipulate the dynamic version of this 2nd formulation, navigate to it using the appropriate button in the ABOVE dynamic sketch; the picture below is static.

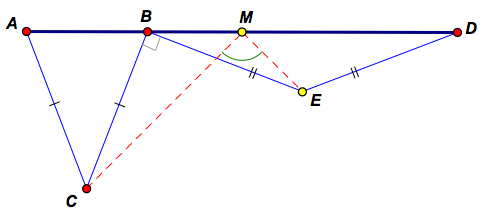
Alternative, equivalent formulation

Challenge: Can you prove either one of these formulations? This extremely rich problem (but deceptively hard problem) can be proved in many different ways, which enhances its beauty and intrigue. If you get stuck, one possible hint is given in the second version above - press the Hint button in the dynamic sketch at the top.

Compare your own solution to this one, 'Application of a generalization of Van Aubel', which includes a link to an interactive sketch as well as a link to a paper in Dutch with 5 different proofs of the result.

A download link to 9 more different proofs in Dutch, zipped together in one file (3 MB), is available to download at 'Further proofs'.

In Sept 2013, my friend and colleague Poobhal Pillay, the Siyanqoba Math Problem Solving Development Coordinator for KwaZulu-Natal High Schools, supplied the following short, elegant proof of the 2nd version above using only the theorem of Pythagoras: 'Poobhal Proof'.

The first formulation of the Klingens problem has also been proposed, slightly differently, on Alex Bogomolny's website in 2017 by Thanos Kalogerakis, Greece, and elegantly proved at: 'A Problem in Pentagon with Supplementary Angles'.

More recently, in 2020, the first formulation of Dick Klingens' theorem resurfaced as the 'Lux Problem'. It was brought to my attention by Hans Humenberger, Austria, and the preceding link to a dynamic sketch of the Lux problem, gives some new proofs as well as revisiting some old ones.

Visit Dick Klingens' website at his Homepage for a many more interesting, geometric results.