Some Napoleon Converses

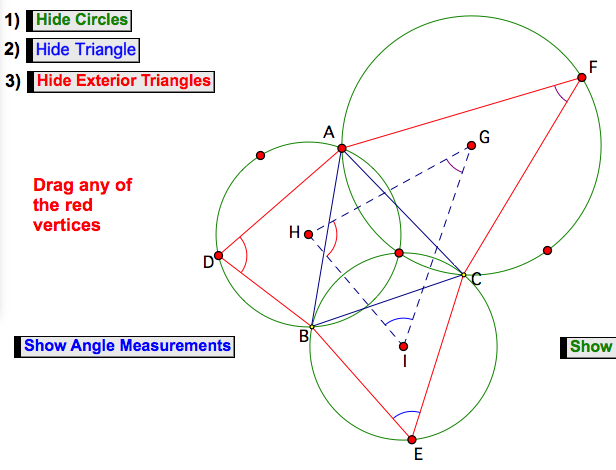
NOTE: Please WAIT while the Applet below loads.

Napoleon Converse
If GHI is an equilateral triangle, and three circles with centres at G, H and I are drawn so that they are concurrent in a point, then equilateral triangles constructed on the sides of triangle ABC formed by the pairwise intersections of circles I and G, G and H, and H and I, respectively, are inscribed in circles G, H and I.

Some Napoleon Converses

Important: To view & manipulate the dynamic versions of the two converses below, navigate to them using the appropriate Link button in the ABOVE dynamic sketch; the pictures below are static.

Napoleon General Converse
If GHI is any triangle, and three circles with centres at G, H and I are drawn so that they are concurrent in a point, and any triangles DBA, BEC and ACF are drawn on the sides of triangle ABC formed by the pairwise intersections of circles I and G, G and H, and H and I, respectively, so that they are inscribed in circles G, H and I, then ∠D = ∠G, ∠E = ∠H, and ∠F = ∠I. (An obvious specialization is that if triangles DBA, BEC and ACF are constructed similar to GHI, then they are inscribed in circles G, H, and I).

Napoleon General Converse

Can you generalize the above result to a quadrilateral and four concurrent circles, and prove your generalization? Can you generalise further?

Specialization: Miquel's Theorem Converse
If GHI is any triangle, and three circles with centres at G, H and I are drawn so that they are concurrent in a point, and any point D on circle G is chosen, and line DB meets circle H again in E, line EC meets circle I again in F, then F, A and D are collinear, and DEF is similar to GHI.

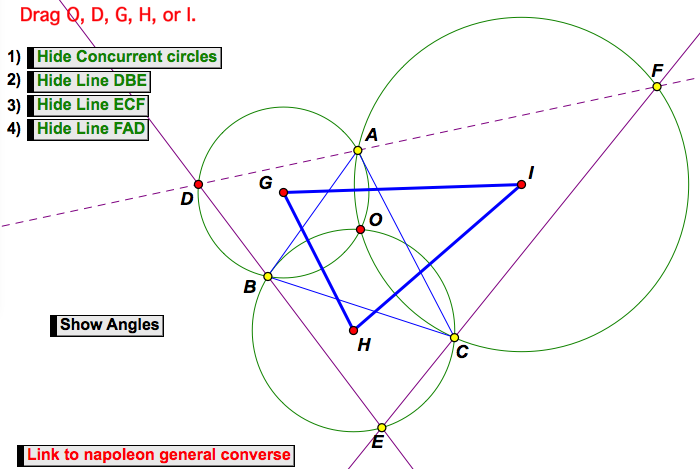
Specialization: Miquel's Theorem Converse

Can you generalize the above Miquel Converse result to a quadrilateral and four concurrent circles, and prove it? Can you generalise further? See "Miquel Variation" for more information.

For several more elaborate converses than those above, read John Wetzel's (1992) AMM paper "Converses of Napoleon's Theorem".