A variation of Miquel's theorem and its generalization

From point O construct equi-inclined¹ lines to the sides (or their extensions) of △ABC, then ADMF, BEMD and CFME are cyclic, and triangle GHI is similar to ABC.
Note ¹: Equi-inclined lines are lines that respectively make equal angles with the sides of a polygon or some other lines.

Miquel variation for triangle

Important: To view & manipulate the dynamic versions of the two generalizations below, navigate to them using the appropriate Link button in the ABOVE dynamic sketch; the pictures below are static.

Further generalization
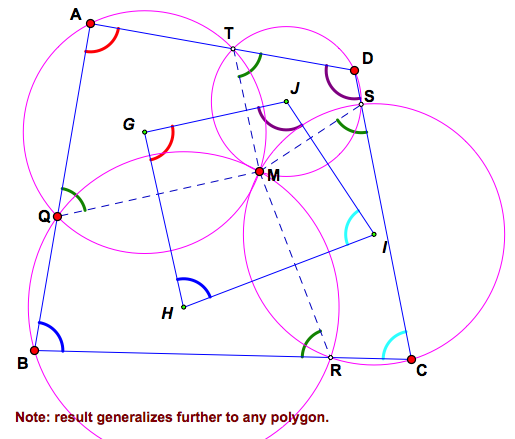
From point M construct equi-inclined lines to the sides (or their extensions) of quadrilateral ABCD, then AQMT, BRMQ, CSMR and DTMS are cyclic (and their circumcircles are concurrent in M), and GHIJ is similar to ABCD.

Miquel variation for quadrilateral

The result generalizes further to any pentagon, hexagon, etc. Read my paper A variation of Miquel's theorem and its generalization in the July 2014 issue of the Mathematical Gazette.

Explore More
Minimum Area of Miquel Circles Centres Triangle

Another, different variation of Miquel
A related, but different 'converse-like' variation of Miquel’s theorem is mentioned without proof for a triangle in [1, p. 135] and [2], but proved in [3] for an n-gon by showing that for n concurrent circles after n spiral similarities of the vertices, centred at the centre of the concurrency, an identity transformation is obtained.
For example: if four circles intersect pairwise and are concurrent in M, then starting with an arbitrary point A on the circumference of one of the circles and continuing to draw straight lines through the other intersections E, F, G and H of the pairwise circles as shown in the figure below, results in A, H and D being collinear, i.e. the construction produces a closed quadrilateral. Though not explicitly mentioned in [3], it is obvious as already shown with the quadrilateral result proven in the preceding result, that the closed quadrilateral ABCD is similar to the one formed by the centres of the four circles, namely, PQRS.
References
1. R.A Johnson, Advanced Euclidean Geometry (Modern Geometry), New York: Dover Publications, (1929), pp. 131-135.
2. D. Wells, Penguin Dictionary of Curious and Interesting Geometry, London: Penguin Books, (1991), p. 184.
3. I.M. Yaglom (translated by A. Shields), Geometric Transformations II, Washington: The Mathematical Association of America, (1968), pp. 46-47, 129-130.

Another different variation of Miquel's theorem

Note that the dynamic sketch for this variation is not very robust and will 'fall apart' due to various construction restrictions of the software, e.g. when dragging point A past point E, etc.

Other examples of results involving equi-inclined lines:
A generalization of Neuberg's Theorem and the Simson line
Equi-inclined Lines Problem
Generalizations of a theorem by Wares