Some other bicentric constructions

Bicentric quadrilaterals are quadrilaterals that have their vertices inscribed on a circle (cyclic) as well as their sides circumscribed around (tangential to) a circle. They therefore have an incircle as well as a circumcircle, and have many interesting geometric properties that can be explored with dynamic geometry.

Probably the most commonly used method to accurately construct a bicentric quadrilateral is based on the following theorem:
In a circumscribed (tangential) quadrilateral ABCD, the lines connecting opposite tangent points to the incircle are perpendicular, if and only, if the circumscribed (tangential) quadrilateral is also cyclic.

More recently, Oxman & Stupel (2020) gave another new, easy way of Constructing a Bicentric Quadrilateral.

Here's another easy method: Start with incircle O and draw two tangents to two arbitrary constructed radii OP and OQ (see below). Construct the intersection of these two tangents, A, and measure/mark ∠A = α. Then draw another arbitrary radius OR and rotate OR by the same angle α to map it to OS (where S = R'). Construct tangents at R and S to meet the other two tangents at B and D, and each other at C. Then ABCD is bicentric.

Some other bicentric constructions

Proof: It follows from the 1st construction above that the opposite angles at A and C are supplementary, which implies ABCD is also cyclic; and hence bicentric.

Published paper: De Villiers, M. (2021). Another Bicentric Quadrilateral Construction. Learning & Teaching Mathematics, No. 31, pp. 40-41.

Using Fuss' theorem: The distance d between the incentre and circumcentre of a bicentric quadrilateral was derived by Nicolaus Fuss (1755-1826) in 1792 and is given by the following formula:
d = √(R² + r² - r √(4R² + r²)) where r and R are respectively the inradius & the circumradius.
In the above sketch click on the 'Link to Fuss construction' button. We can now use this formula to construct a bicentric quadrilateral as follows:
1) Start with two segments R = AB and r = CD for the respective radii of the circumcircle and incircle.
2) With your software, calculate the distance d between the circumcentre & incentre with Fuss' formula. Construct circle E with radius R = AB, and with E as centre also, construct another circle with radius d.
3) Choose a point F on this latter circle and with it as centre, construct a circle with radius r = CD.
4) Then construct a tangential quadrilateral to the incircle by first constructing a tangent GH with G and H the intersection of this tangent with the circumcircle. Next construct the tangents GJ and HI to obtain a tangential quadrilateral GHIJ.
5) By Poncelet's porism one can drag either of K and/or F to get an infinite family of bicentric quadrilaterals GHIJ for these two circles. One can also drag the respective radii AB and CD to change the distance between the centres.

Challenge: Can you find other methods of constructing a bicentric quadrilateral?

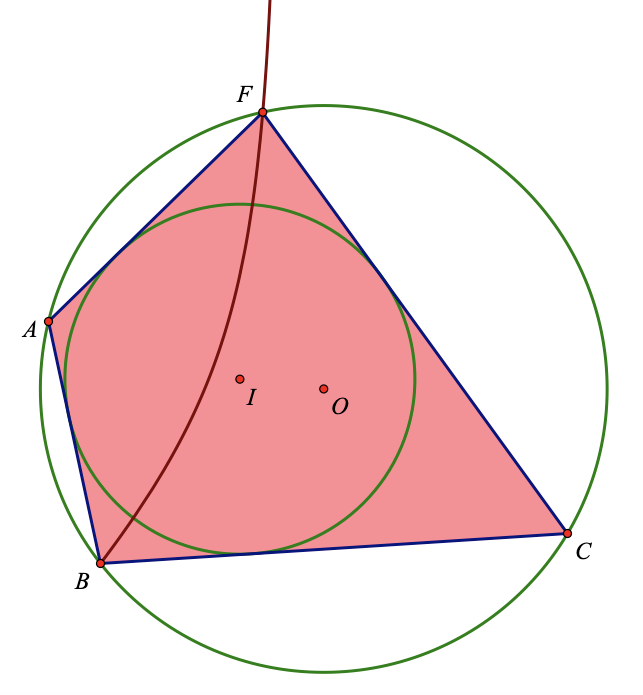
Dan Bennett's Construction A long-time colleague & friend, Dan Bennett, who is a Math Teacher at John O’Connell HS, San Francisco CA, recently sent me (2 June 2021) the following novel bicentric quadrilateral construction using Sketchpad (see sketch below):
1) Construct rays BA and BC and angle bisector of ∠B. The points A, B, and C will be three free vertices of the final quadrilateral (that can be dragged).
2) Construct a point D on the angle bisector and drop a perpendicular to one of the rays. Construct a circle to this intersection that will be tangent to the two rays.
3) From A and C, construct the other lines tangent to the circle you just made. Construct point E at their intersection. ABCE is now a quadrilateral that has an incircle.
4) Construct the circumcircle of ABC.
5) Construct the locus of point E as point D moves on the angle bisector. This is a hyperbola, because BA + CE = BC + AE.
6) Construct point F at the intersection of the hyperbola and the circumcircle. ABCF is the desired bicentric quad.
This construction appears to affirm the plausible conjecture that for any three non-collinear points A, B, and C, there exists a unique fourth point F such that ABCF is bicentric.

Notes:
i) Since the Sketchpad sketch involves the intersection of a locus (of a conic) and a circle, it unfortunately does not convert to WebSketchpad. However, Sketchpad users can download & unzip the Sketchpad sketch from here: Bennett GSP Construction.
ii) Dan has now also discovered that two vertices of the quadrilateral are the foci of the hyperbola - so he was able to do the same construction in GeoGebra using the hyperbola tool instead of the locus tool. However, since the hyperbola intersects the circumcircle in four points, only one of which is the correct fourth vertex of the quad, the construction breaks very easily. The intersection bounces among the four possible locations seemingly randomly. Here's his dynamic GeoGebra sketch online: Bennett Construction 2.
iii) Users of other dynamic geometry software are invited to duplicate Dan Bennett's construction for themselves.