Generalizations of a theorem by Wares¹

NOTE: Please WAIT while the applet below load.

Generalization 1: Choose arbitrary points X, Y and Z. If perpendiculars are dropped from A, B and C to line segments YZ, XZ and XY, respectively, and if U, V and W are the intersections of these perpendiculars as indicated, then ∆UVW is similar to ∆XYZ. (¹See A theorem of Wares.)

Arbitrary points X, Y and Z

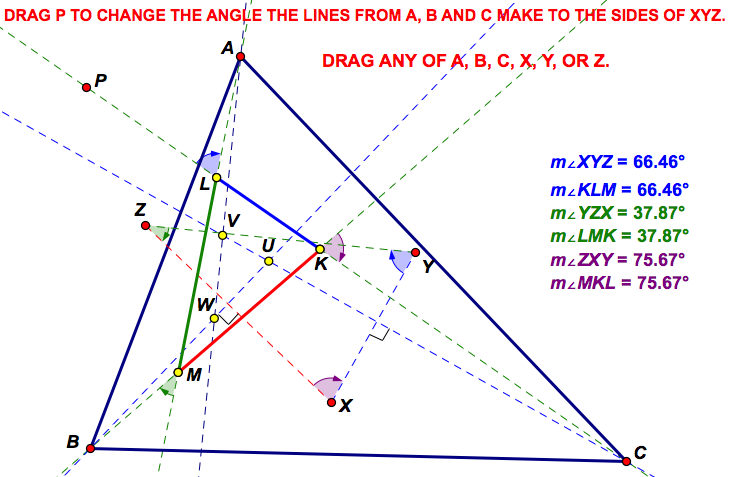
Generalization 2: If equi-inclined (making same angles) lines are dropped from A, B and C to line segments YZ, XZ and XY, respectively, and if K, L and M are the intersections of these equi-inclined lines as indicated, then ∆KLM is similar to ∆XYZ. (Point P can be dragged in the linked sketch above to change the angle the equi-inclined lines make with the sides of XYZ.)

Note: The Equi-inclined Lines Problem in the Student Explore section can be viewed as a special case of the above generalization 2, and is immediately obtained by moving each of X, Y and Z respectively to a vertex of the original triangle.

Important: To view & manipulate the dynamic version of this generalization, and the next one, navigate to them using the appropriate buttons in the ABOVE dynamic sketch; the two pictures below are static.

Equi-inclined lines to sides of XYZ

Generalization 3: Choose arbitrary points E, F, G and H. If perpendiculars are dropped from A, B, C and D to line segments HE, EF, FG and GH respectively, and if P, Q, R and S are the intersections of these perpendiculars as indicated below, then PQRS is equi-angled to EFGH.

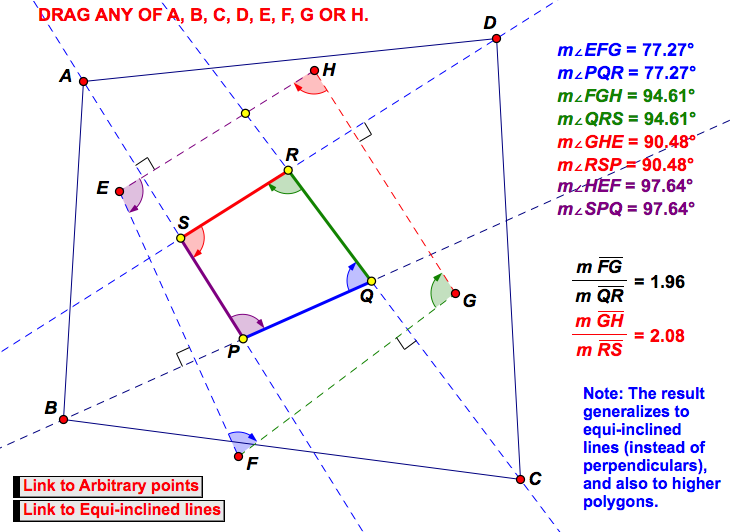
Generalization to quadrilateral

Regarding the above, read my paper in The Scottish Mathematical Council Journal (2012), Generalizing a theorem of Arsalan Wares.