Some Corollaries to Van Aubel Generalizations

Corollary 1
If similar rectangles with centres E, F, G and H are erected externally on the sides of quadrilateral ABCD as shown, then the midpoints of the sides of EFGH form a rectangle similar to the four similar rectangles. (Furthermore, the midpoints of the sides of JKLM, form a rhombus with the angle(s) of its sides equal to the angle(s) of the diagonals of the similar rectangles).

Widgets

Similar Rectangle Corollary

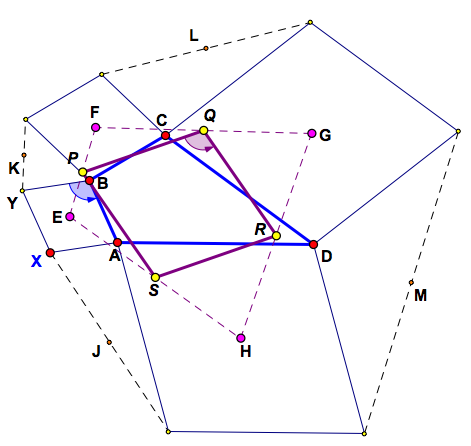
Corollary 2
If similar rhombi with centres E, F, G and H are erected externally on the sides of quadrilateral ABCD as shown, then the midpoints of the sides of EFGH form a rhombus similar to the four similar rhombi. (Furthermore, the midpoints of the sides of JKLM, form a rectangle with sides in the ratio YA/XB of the diagonals of the similar rhombi).

Important: To view & manipulate the dynamic version of this result, navigate to it using by clicking on the 'Link to similar rhombi' button at the bottom of the ABOVE dynamic sketch; the picture below is static.

Similar Rhombi Corollary

Corollary 3
If similar parallelograms with centres E, F, G and H are erected externally on the sides of quadrilateral ABCD as shown, then the midpoints of the sides of EFGH form a parallelogram similar to the four similar parallelograms. (Furthermore, the midpoints of the sides of JKLM, form a parallelogram with sides in the ratio YA/XB, and the angle(s) of its sides equal to the angle(s) of the diagonals of the similar parallelograms, but it is not (necessarily) similar to the other parallelograms).

Important: To view & manipulate the dynamic version of this result, navigate to it by clicking on the 'Link to similar parallelograms' button in the 2ND (similar rhombi) page of the above dynamic sketch; the picture below is static.

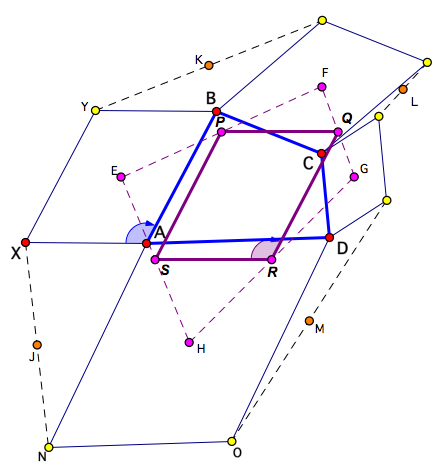
Similar Parallelogram Corollary

Challenge
1) Can you explain why (prove that) the above results are true?
2) Drag the vertices so that ABCD becomes concave or crossed. Can you also explain why (prove) that the result remains true in these cases?

Related Links
Van Aubel's Theorem and some Generalizations
Twin Circles for a Van Aubel configuration involving Similar Parallelograms
An associated result of the Van Aubel configuration and some generalizations
Quadrilateral Balancing Theorem: Another 'Van Aubel-like' theorem
A Fundamental Theorem of Similarity
Some Variations of Vecten configurations
A Vecten area variation (Cross's theorem) & generalizations to quadrilaterals