Matric Exam Geometry Problem - 1949
(A variation of Reim's theorem)

"The definition of a good mathematical problem is the mathematics it generates rather than the problem itself." — Andrew Wiles from an interview for PBS website on the NOVA program, 'The Proof'.

The following exploration is generalized from a question in the Mathematics Paper 2 of the 1949 National Senior Examinations for Grade 12 for the (then) Union of South Africa.

Matric Problem (Given)
Given any trapezium ABCD with AB // DC and line EF constructed as indicated so that ∠AEF = ∠DCF.

Exploration
1) Click on the 'Show Angles' button to display the angle measurements of ∠'s BEC and AFD. What do you notice?
2) Explore your observation in 1) above by dragging any of A, B, C, D or E. Can you deductively explain (prove) why your observation is true?
3) Is the result still valid if E is dragged 'outside' AD onto its extensions on both sides? What if point D is dragged towards C, and then past C? Is the result still valid?^1
1 Note that when point D is dragged past C, the given condition becomes ∠AEF = 180° - ∠DCF.
4) Challenge: Can you deductively explain (prove) your observations above?

Matric Exam Geometry Problem - 1949

Further exploration
5) Can you formulate alternative, equivalent versions of the result? Can you create your own dynamic geometry sketch?
6) When, or rather where, is ∠BEC a maximum as E is dragged along line AD? Can you determine the optimal position?
Hint: If you get stuck with 6) above, go to this dynamic sketch Determining maximum angle. Or use it to check & compare your solution.
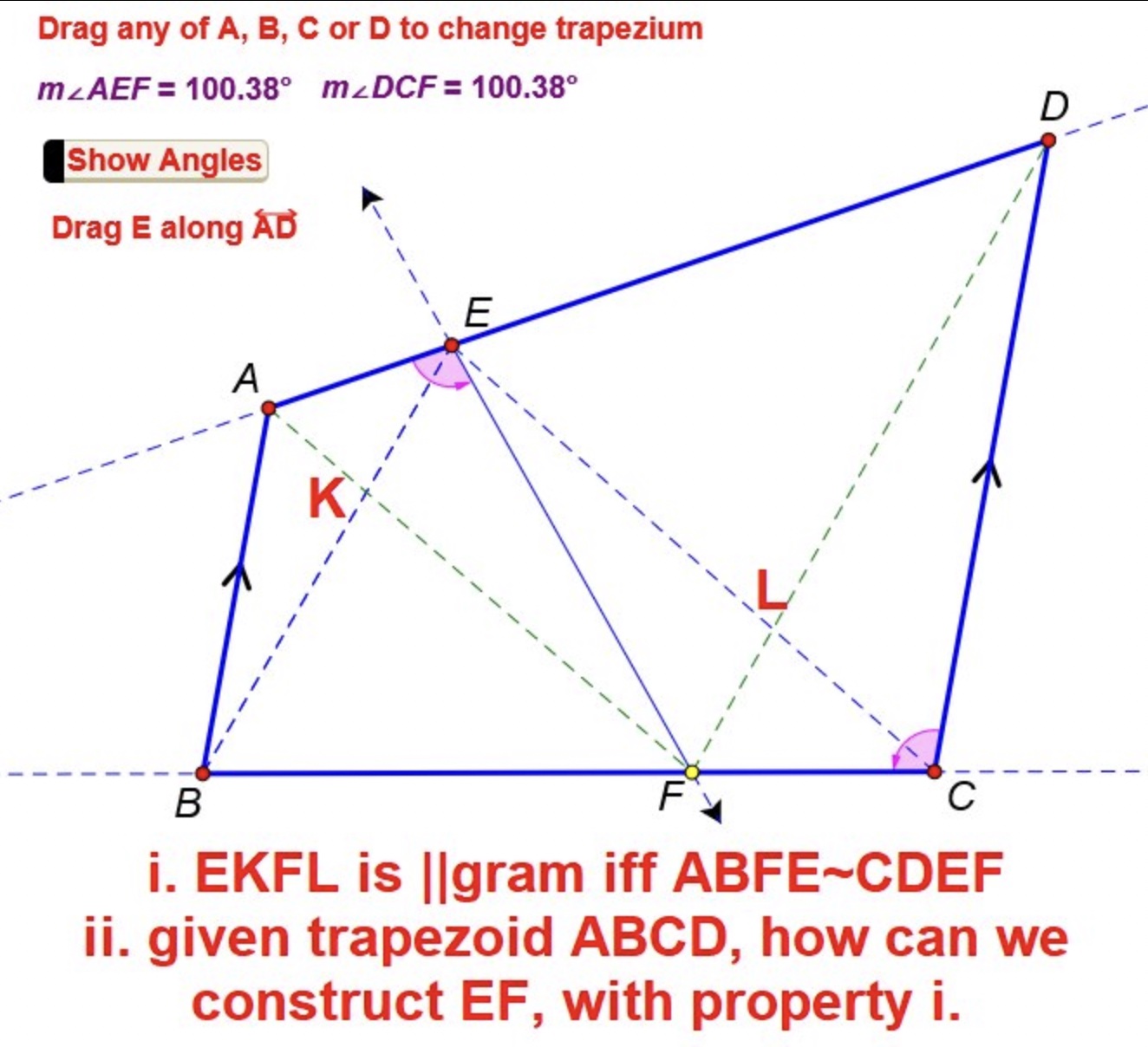
7) Recently (Jan 2024) on my Facebook page, colleague Thanos Kalogerakis from Kiáto, Greece suggested another variation, which is shown below.
Hint: If you get stuck with 7) above, go to this link Thanos solution - construction of EF.

Published Paper
Check your explorations for 1)-6) above, by reading my 2015 paper in At Right Angles and Learning and Teaching Mathematics at "Flashback to the Past: a 1949 Matric Geometry Question".

Reim's theorem
Thanos Kalogerakis also kindly brought to my attention that the basic result mentioned at the start is a variation of what is apparently known as Reim's theorem. It is named after Anton Reim (1832–1922), a Czech mathematician. Read more about this theorem at the following links:
Art of Problem Solving: Reim's Theorem
Art of Problem Solving: Lemmas in AoPS Geometry by Evan Chen
Art of Problem Solving: Used in solution for IMOC 2019 G5
Cut the Knot: Reim's Similar Coins
Maths Olympian: Reim's theorem
Pleasanton Math Circle: Notes on Cyclic Quadrilaterals.
Note: If anyone knows more about the origin of this interesting theorem or applications of it, please let me know.

Related Links
Matric Exam Geometry Problem - 1949: Maximizing ∠BEC
All parabola are similar - i.e. have the same shape
Cyclic Hexagon Alternate Angles Sum Theorem
A generalization of the Cyclic Quadrilateral Angle Sum theorem
Angle Divider Theorem for a Cyclic Quadrilateral
Semi-regular Angle-gons and Side-gons: Generalizations of rectangles and rhombi
Alternate sides cyclic-2n-gons and Alternate angles circum-2n-gons
Nine-point centre (anticentre or Euler centre) & Maltitudes of Cyclic Quadrilateral
An extension of the IMO 2014 Problem 4

Back to "Dynamic Geometry Sketches"

Back to "Student Explorations"

Created by Michael de Villiers, 13 August 2015; updated to WebSketchpad 18 Jan 2024, updated 25 Jan 2024.