Cyclic Hexagon Alternate Angles Sum Theorem
Historical Note: This (convex) cyclic hexagon theorem does not appear in Euclid's "Elements", and was apparently first discovered and proved by Duncan Gregory who in 1836 published it in the Cambridge Mathematical Journal.
Cyclic Quadrilateral Note: This result is a generalization to cyclic hexagons of the familiar result for a cyclic quadrilateral ABCD, namely, ∠A + ∠C = ∠B + ∠D (which is equal to 180o when it is convex, and using directed angles, equal to 360o when crossed (see De Villers, 1994, 1999)1). While it is usually formulated at high school level for convex cyclic quadrilaterals that the sum of opposite angles are supplementary, it is actually more convenient to regard the angles involved as 'alternate' angles, which more clearly illustrates the hexagon generalization above, and to cyclic 2n-gons in general.
Challenge
1) Can you explain why (prove that) the sum of the alternate angles of a cyclic hexagon remain equal, specifically that ∠A + ∠C + ∠E = ∠B + ∠D + ∠F?
2) If not, click on the given HINT button in the sketch.
3) Can you prove the result in more than one way?
(Check your solutions against those in this 2017 Multiple Solutions paper by Duncan Samson who tried this problem with his high school class at St. Andrews & DSG. More recently in 2023, Yiu-Kwong Man provided a nice Visual Proof of the convex case.)
Converse
4) Is the converse true? I.e. if ∠A + ∠C + ∠E = ∠B + ∠D + ∠F does it imply that ABCDEF is cyclic? Investigate & prove or disprove.
5) Check your answer in regard to 4) by reading this paper Recycling cyclic polygons dynamically.
Further Generalization
6) Can you generalize further to (convex) cyclic octagons, cyclic decagons, etc.? Explore dynamically on your own using appropriate software!
Dual Result
7) Can you formulate a similar dual result for a tangential/circumscribed hexagon involving its sides? Investigate further!
Related Links
8) Regarding 6) & 7) above, go here for more information: Further Generalization & Dual and Circumscribed Hexagon Alternate Sides Sum theorem respectively.
Crossed Cyclic Hexagon Investigation
9) What happens to the sum of the alternate angles when the hexagon ABCDEF becomes crossed?
10) To investigate this question click on the 'Link to crossed cyclic hexagon - directed angles' button to navigate to a new sketch. This sketch uses 'directed angles' which means that according to the same convention used in trigonometry, counter-clock wise rotations (angles) are regarded as positive and counter-clock wise ones as negative.
Investigate: Drag any one of the vertices past an adjacent one. What do you notice about the sum of the alternate angles now? Ensure that you at least drag your sketch into each of the three configurations below.
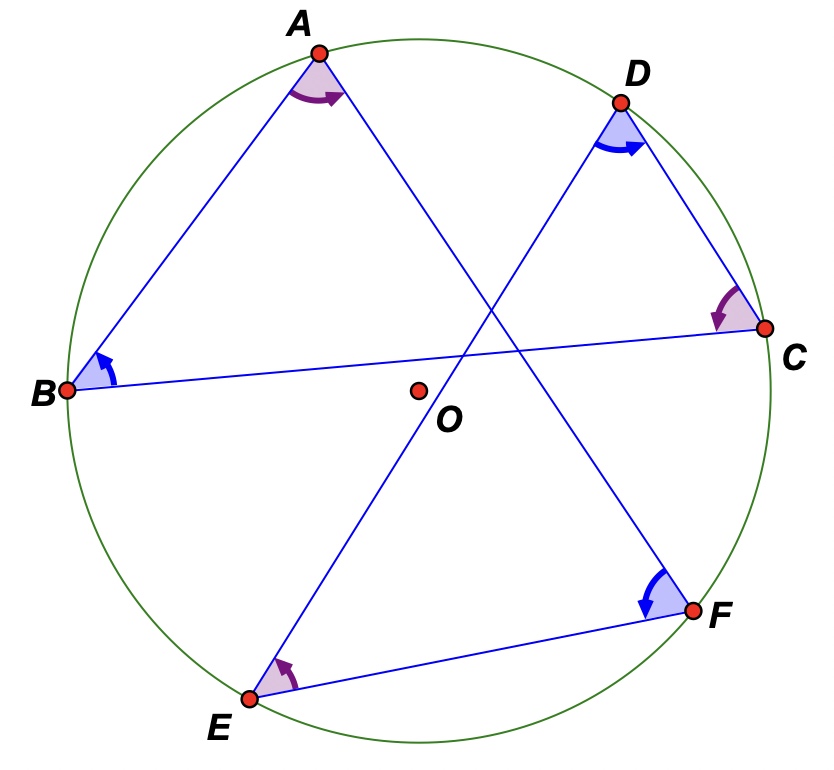
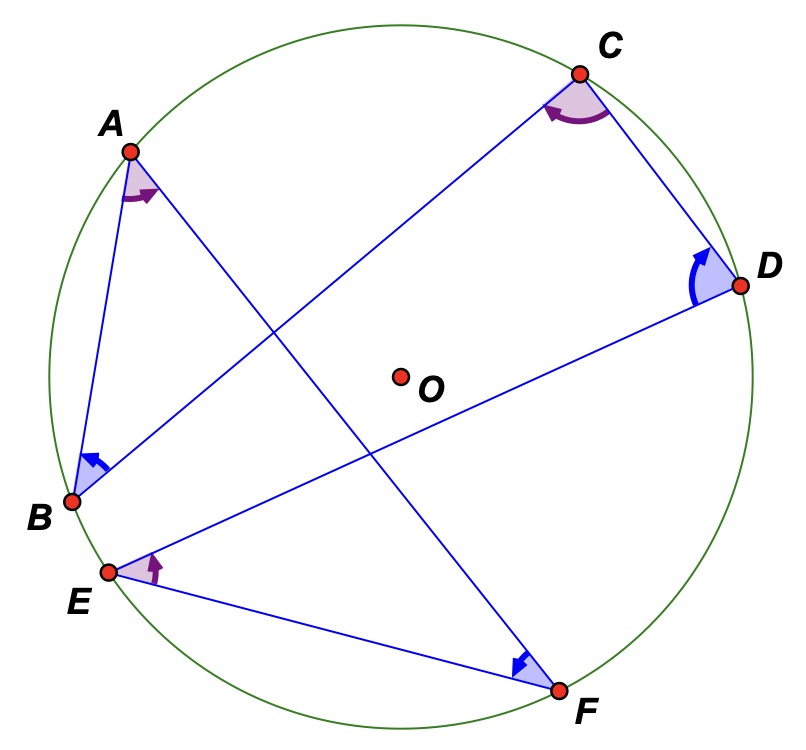
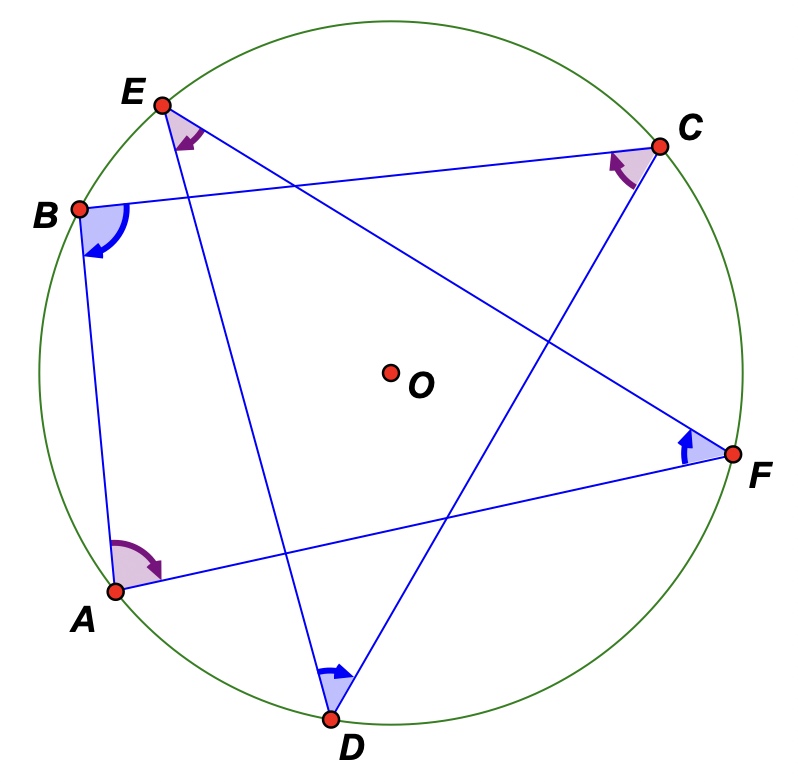
11) Challenge: Can you explain why (prove that) your observations in 10) above are true?
12) Check: Click on the 'Link to Check Findings' button to check your findings in 10) & 11) above.
Footnote to Cyclic Quadrilateral Note
1If angles for a crossed cyclic quadrilateral are measured in the same way as with the crossed hexagon above, using directed angles, and not allowing any reflexive angles, but measuring negative angles instead, then the sum of alternate angles for a crossed cyclic quadrilateral would be 0o. This shows how the choice of one's definitions in mathematics can profoundly influence one's results.
Published Paper
A paper Investigating Alternate Angle Sums of Crossed Cyclic Hexagons of mine related to the above has been published in the Learning & Teaching Mathematics journal, No. 35, Dec 2023, pp. 28-31.
...........
Using GeoGebra to investigate alternate angle sums in crossed cyclic hexagons
GeoGebra Classic 6 automatically measures angles using directed angles in the background and can also measure reflexive angles (i.e. greater than 180o). See the PDF Cyclic Hexagon Illustrations with GeoGebra to see some examples of how it is different from the Sketchpad sketches above.
As can be seen in the preceding PDF link, for crossed cyclic hexagons, the sum of the alternate angles with GeoGebra can be 540o, 720o and 900o; so there are also three different cases like with Sketchpad above (where the three measured sums are -180o, 0o and 180o). The difference is due to GeoGebra measuring directed angles greater than 180o whereas Sketchpad not only measures, but also displays negative angles, and is restricted to only measuring directed angles smaller than 180o.
However, since GeoGebra takes the absolute values of the directed angles, it does not display negative angles, and in some configurations, the two sums of alternate angles are unfortunately not displayed as being equal. One example of this issue is given in the PDF at the preceding link where the sum of one set of alternate angles is 540o while the other is given as 180o.
Additional References
a) A classroom activity and guided proof of the (convex) cyclic hexagon result is also given in the FREE DOWNLOAD of Rethinking Proof with Sketchpad (1999, 2003, 2012), pp. 50; 162-163.
b) Proofs and generalizations of these results are also given in Some Adventures in Euclidean Geometry (1994), as well as generalizations to cyclic 2n-gons with crossed sides. The book is available for purchase as a downloadable PDF, printed book or from iTunes for your iPhone, iPad, or iPod touch, and on your computer with iTunes.
c) De Villiers, M. (2020). The Value of using Signed Quantities in Geometry Learning & Teaching Mathematics, no. 29.
Related Links
Crossed Quadrilateral Properties
Interior angle sum of polygons (incl. crossed): a general formula
Investigating a general formula for the interior angle sum of polygons (A suggested guided learning activity starting with LOGO (turtle) geometry)
A generalization of the Cyclic Quadrilateral Angle Sum theorem
Alternate Sides Sum Circumscribed Hexagon
Parallelogram Distances
2D Generalizations of Viviani's Theorem
Angle Divider Theorem for a Cyclic Quadrilateral
Side Divider Theorem for a Circumscribed/Tangential Quadrilateral
Conway’s Circle Theorem as special case of Side Divider Theorem
Pitot's Theorem (alternate sides sum theorem for a tangential quadrilateral)
Tangential Quadrilateral Theorem of Gusić & Mladinić
Semi-regular Angle-gons and Side-gons: Generalizations of rectangles and rhombi
**************
Free Download of Geometer's Sketchpad
Back to "Dynamic Geometry Sketches"
Back to "Student Explorations"
Created in 2008; modified by Michael de Villiers, 24 March 2012; updated 1 Sept 2020 with WebSketchpad; updated 27 June 2023; 4 July 2023; 12 Dec 2023.