A generalization of Neuberg's Theorem to polygons
Related Generalizations of Viviani's Theorem
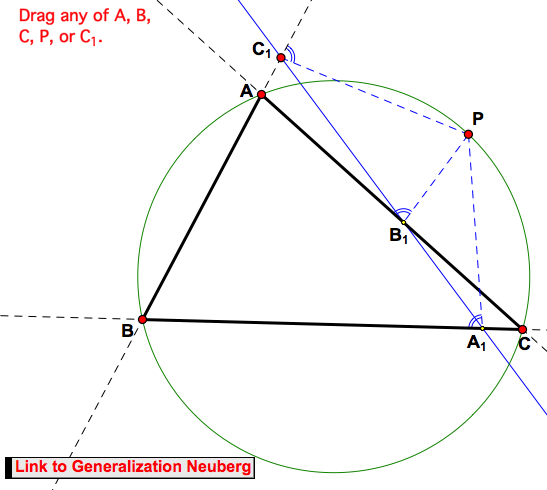
A generalization of the Simson-Wallace line (1799)
From point P on the circumcircle of ΔABC construct lines to the sides (or their extensions) of ΔABC so that they respectively form three equal angles with the sides. Then these three "feet" lie on a straight line, the 'Miquel line'.
Note
Read more about the historical background of the Simson-Wallace line, named after two 18th century British mathematicians.
Important: To view & manipulate the DYNAMIC version of the Simson-Wallace generalization, navigate to it using the appropriate button in the dynamic sketch right at the TOP; the picture below is static.
A generalization of the Simson-Wallace line
Explore the further or related generalizations below and also try to explain why (prove) why they are true.
More properties of the generalised Simson-Wallace line
Miquel Deltoid (or Hypocycloid)
Published Paper
Download an article of mine from the Mathematical Gazette (2002) giving proofs of the results above at From nested Miquel triangles to Miquel distances.
Explore More
Maximising the Area of the 3rd Pedal Triangle in Neuberg's theorem
More Equi-inclined lines
Other examples of results involving equi-inclined lines:
A variation of Miquel and its generalization
Equi-inclined Lines Problem
Generalizations of a theorem by Wares
Related Investigation
The paper below explores some properties of several sequences of nested triangles, among which is Neuberg's theorem.
Ismailescu, D. & Jacobs, J. (2006). On Sequences of Nested Triangles. Periodica Mathematica Hungarica, Vol. 53 (1–2), pp. 169–184.
Other Related Links
Carnot's (or Bottema's) Perpendicularity Theorem & Some Generalizations
Power Lines of a Triangle
Power Lines Special Case: Altitudes of a Triangle
Clough's Theorem (a variation of Viviani) and some Generalizations
2D Generalizations of Viviani's Theorem
Parallelogram Distances
Some Variations of Vecten configurations
Maximising the Area of the 3rd Pedal Triangle in Neuberg's theorem
***************
Free Download of Geometer's Sketchpad
***************
Back to "Dynamic Geometry Sketches"
Back to "Student Explorations"
Created by Michael de Villiers, 21 January 2010. Changed to WebSketchpad, 21 April 2020; modified 9 August 2021; updated 14 May 2023; 20 July 2023; 18 March 2025.