Sylvie's Theorem

For a convex quadrilateral ABCD in the plane, if each vertex is joined to the midpoint along the alternate side (measured say anti-clockwise) to form a quadrilateral EFGH as shown, then 1/5 area ABCD >= area EFGH > 1/6 area ABCD, and equality holds when EFGH is a trapezium.

Sylvie's Theorem

To view the equality in Sylvie's Theorem, namely, when 5 x area EFGH = area ABCD, click on the Link to Equality case example Button in the dynamic sketch above.

Notes:
1) In the (1999/2003) Preface of my Rethinking Proof with Sketchpad book by Key Curriculum Press (now at McGraw-Hill), it is described how in 1995, a University of Durban-Westville (now University of KwaZulu-Natal) Masters student (and colleague) of mine, Sylvie Penchaliah, during a class investigation, made the conjecture that 1/5 area ABCD >= area EFGH in relation to the Areas Investigation on pp. 73-75 in my book.
2) Sylvie's Theorem also appears as a conjecture in a paper by Keyton, M. (1997). Students discovering geometry using dynamic geometry software. In J. King & D. Schattschneider (Eds.), Geometry turned on! Dynamic software in learning, teaching and research (pp.63-68). Washington, DC: The Mathematical Association of America.
3) A proof of the result by Avinash Sathaye, Carl Eberhart and Don Coleman from the Univ. of Kentucky in 2002 is available at Coleman proof.
4) Another proof and further extension by Marshall, Michael & Peter Ash in 2007 in an article in the Mathematical Gazette, 93(528), can be found at Ash proof.

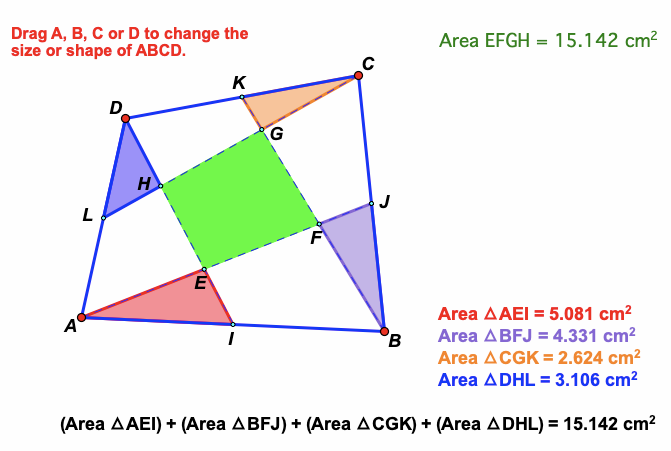
More recently, in a post on 26 April 2021 in the Facebook Group 'Romantics of Geometry', Hasan Ata from Turkey, mentioned the lovely related result shown in the diagram above.
5) Can you prove this result? Can you maybe use this result to prove the general identity of Sylvie's theorem?

Check & compare your own proof of Hasan Ata's theorem with his written proof at Hasan Ata proof.

Related Links
Another parallelogram area ratio
An Area Preserving Transformation: Shearing
International Mathematical Talent Search (IMTS) Problem Generalized
Some Parallelo-hexagon Area Ratios
Area Parallelogram Partition Theorem: Another Example of the Discovery Function of Proof
Finding the Area of a Crossed Quadrilateral