International Mathematical Talent Search (IMTS) Problem Generalized

Problem
In the Mathematics & Informatics Quarterly, Sept 1996, pp. 180-182 the following problem from the International Mathematical Talent Search (IMTS) 19 was given in relation to the dynamic figure below:
"Determine the area of the shaded octagon as a fraction of the area of the square, where the boundaries of the octagon are lines drawn from the vertices to the midpoints of opposite sides."

Explore
1) Click on the 'Show Areas' button below to view the ratio between the two areas concerned. Drag any of the red vertices to explore.
2) Note that the formed octagon is not regular. However, it has all sides equal and alternate angles are equal as can be seen by clicking on the 'Show Side Lengths' and 'Show Angles' buttons. The shaded octagon is therefore what I've called a semi-regular side-gon, specifically in this case, a 'semi-regular side-octagon' - which is a generalization to 2n-gons of the concept of a rhombus.

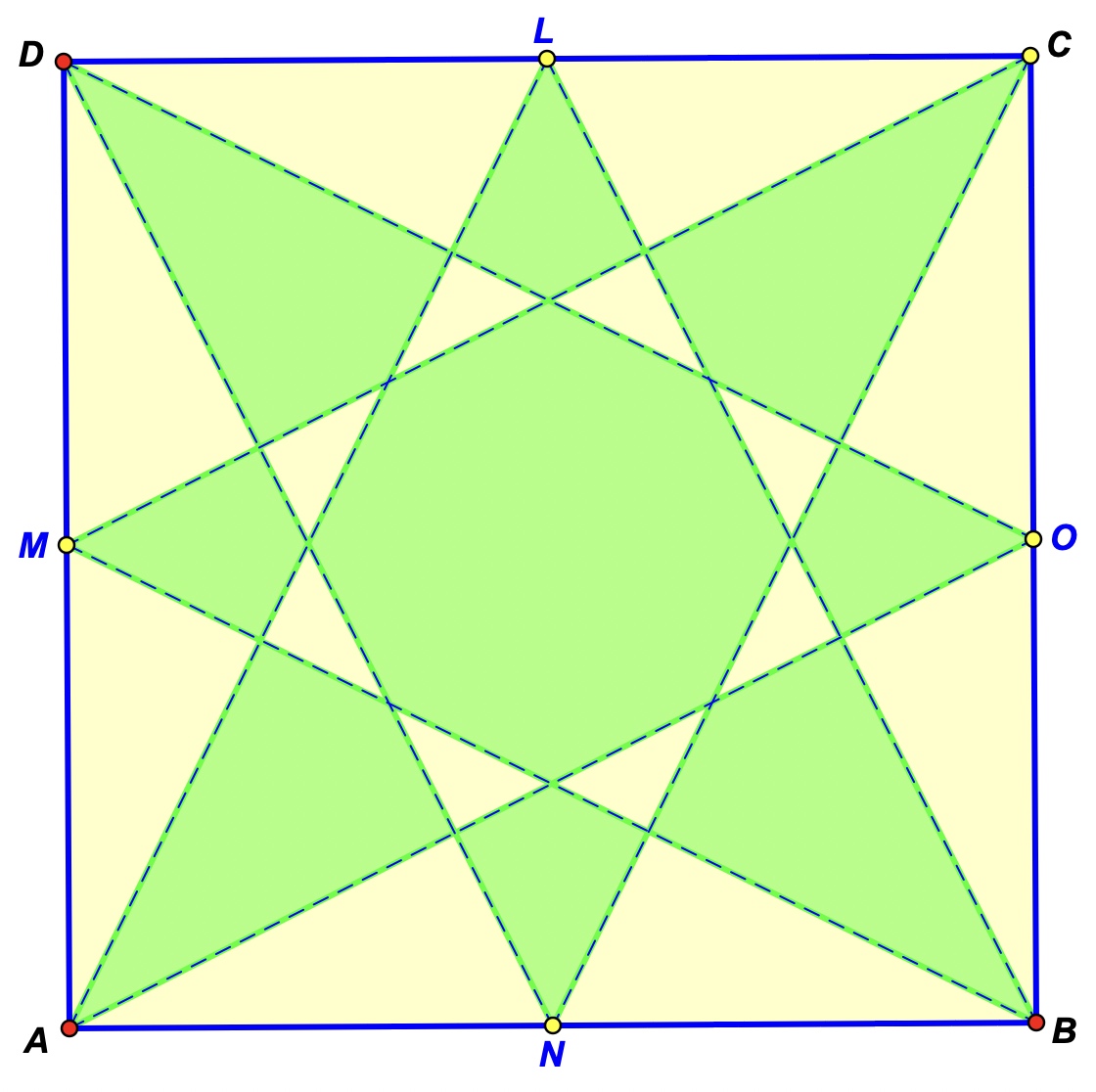
IMTS Problem Generalized

Challenge
3) Can you explain why (prove that) the area ratio observed above is invariant (constant)? Can you explain (prove) it in more than one way?

Generalize Further
Since any square can be sheared and stretched on to a parallelogram (and vice versa), and the midpoints of sides and ratio of areas are both affine invariants, the result immediately generalizes to a parallelogram. Click on the 'Link to parallelogram' button above to navigate to a dynamic sketch illustrating this relationship. Drag any of the red vertices to explore.

Generalize Even Further
4) What happens if instead of bisecting the sides of a parallelogram, each of the sides are divided into three equal parts? Click on the 'Link to parallelogram thirds' button above to navigate to a dynamic sketch illustrating one possible example of such a case. Drag any of the red vertices to explore.
5) What happens if each of the sides are divided into four equal parts? Click on the 'Link to parallelogram fourths' button above to navigate to a dynamic sketch illustrating a case similar to that in 3) above.
6) Can you explain why (prove) your observations in 4) and 5) above are true?
7) Can you generalize further by finding and proving a general formula?

References
De Villiers, M. (1999). A Generalization of an IMTS Problem. KZN Mathematics Journal, 4(1), March, 12-15.
De Villiers, M. (2012). LTM Cover Diagram, February 2006: A semi-regular side-gon. Learning & Teaching Mathematics, no. 12 (June), 34-35.

Other variations
It is quite easy to find many different area ratio problems of this kind and readers are invited to explore some on their own. Below are some other examples to explore.
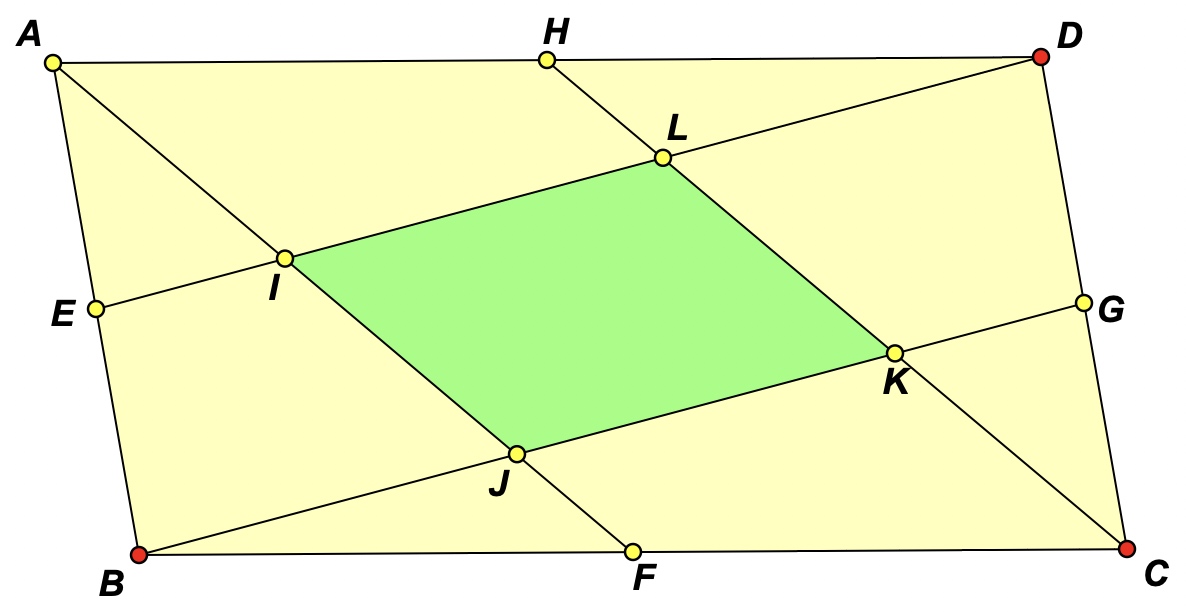
8) Determine the ratio between the parallelogram and the shaded quadrilateral formed by lines drawn from the vertices of the parallelogram to the midpoints of the sides as shown below. (This problem was also used in my Rethinking Proof book and a dynamic geometry sketch is available for the reader at Another parallelogram area ratio.)

9) Determine the ratio between the parallelogram and the shaded parallelo-octagon formed by lines drawn from the vertices of the parallelogram as shown below to: a) thirds of the sides, and b) fourths of the sides. Can you prove these results & generalize further?

.......

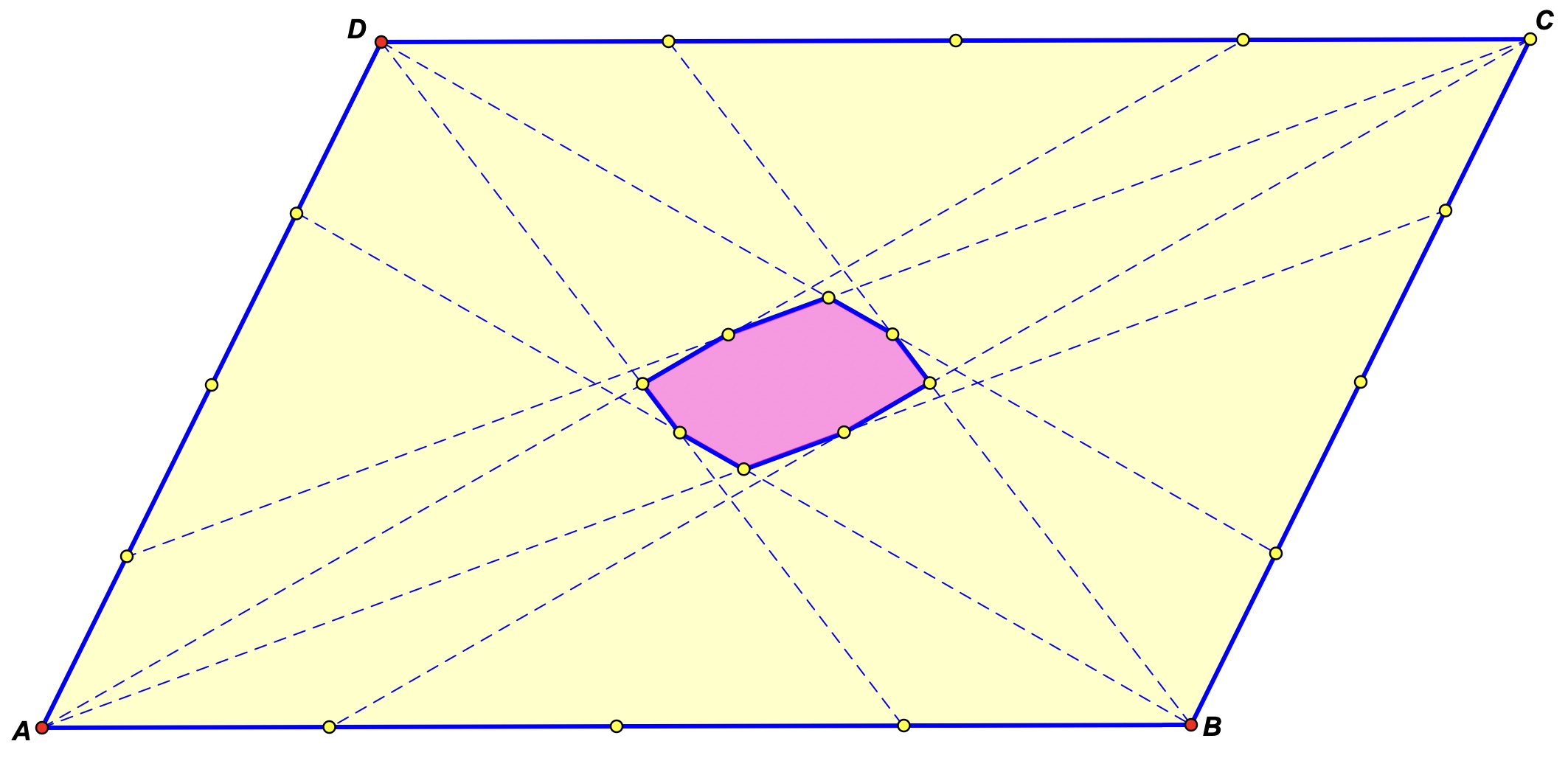
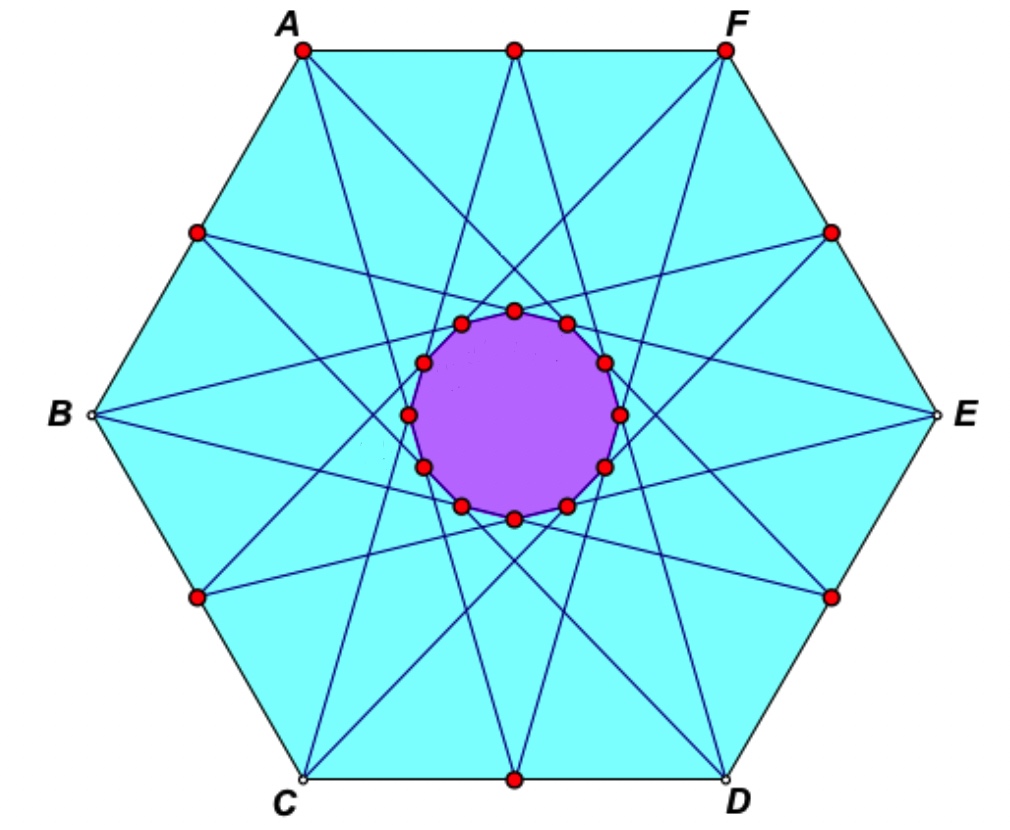
10) Determine the ratio between the regular hexagon and the shaded semi-regular side-dodecagon formed by lines drawn from the vertices of the hexagon to the midpoints of the sides as shown below. Can you find and prove a general formula for this area ratio & generalize further for any regular 2n-gon and its associated interior semi-regular side-gon?

11) Determine the area of the crossed octagon ALBMCNDO as a fraction of the area of the square ABCD, where L, M, N, O are the midpoints of the sides of the square as shown below.

Check or compare your solution to 11) above with the dynamic sketch & discussion here.

Free Download of Geometer's Sketchpad

***********

Back to "Dynamic Geometry Sketches"

Back to "Student Explorations"

Created by Michael de Villiers, approx. 2000, updated with WebSketchpad, 4 Oct 2023; updated 9 October 2023.