Converse of Tangent-Secant Theorem (Euclid Book III, Proposition 36)

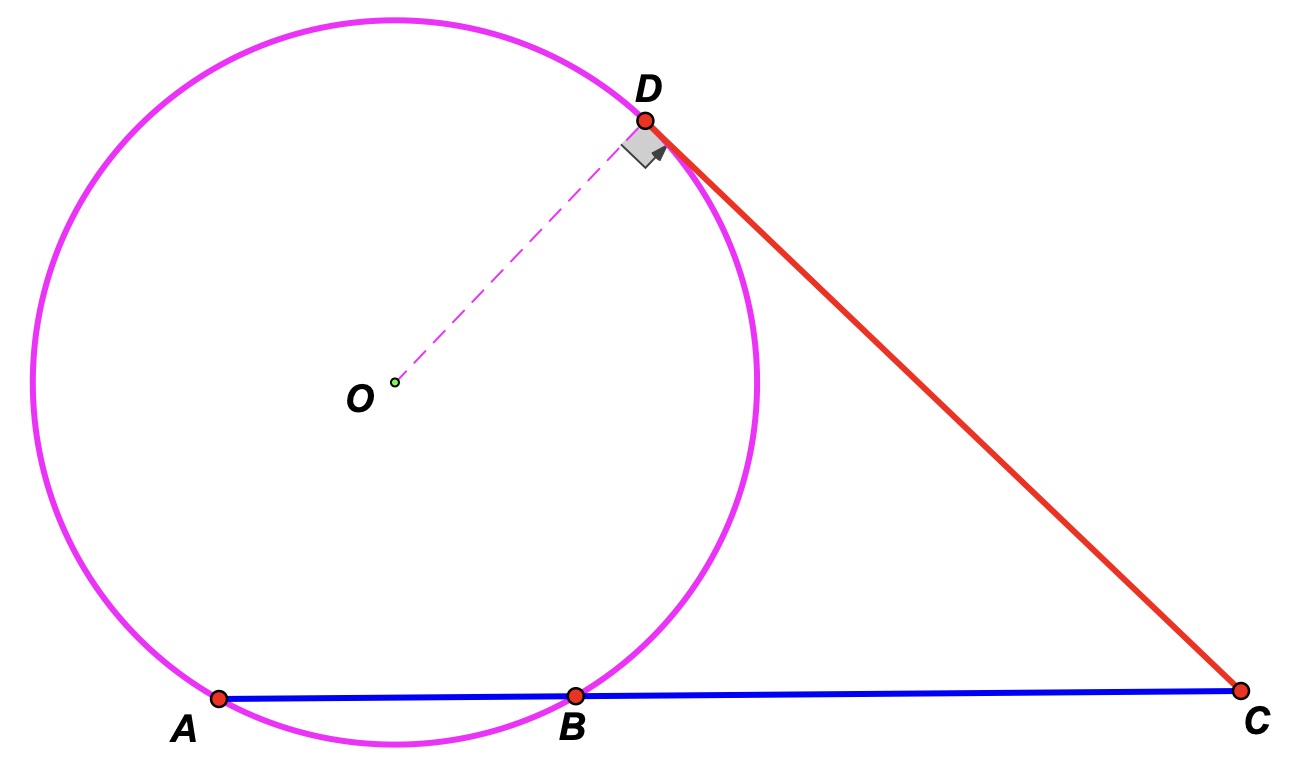
Tangent-Secant Theorem (Euclid Book III, Proposition 36)
Proposition 36 from Euclid Volume III used to appear in the geometry part of the South African High School Curriculum more or less until the mid 1980's.
It is often called the 'tangent-secant' theorem & can be stated more simply than Euclid's version as follows: If a tangent segment CD and a secant segment CA are drawn to a circle from an external point, then the square of the measure of the tangent segment CD is equal to the product of the secant segment CA and its external portion CB. Specifically, CD² = CB x CA.

Converse of Tangent-Secant Theorem
Apparently less well-known is that one can formulate an interesting & useful converse to this theorem as shown in the dynamic sketch below:
1) Given an arbitrary segment AC with an arbitrary point B on it.
2) Note that the measurements of AC and BC are given.
3) Next construct CD = √(AC x BC) by clicking on the 'Show Calculations' button.
4) Next click on the 'Show Circumcircle ABD' button.
5) What do you notice? Check your conclusion thoroughly by dragging.
6) Formulate your conjecture from 5) above.

Converse of Tangent-Secant Theorem

Challenge
7) Can you explain why (prove that) Euclid III, prop. 37, and its converse, is true?
8) Can you explain/prove them in more than one way?
Hint: Try using similarity. Alternatively, a proof of Euclid III, prop. 36 is given at the bottom of this webpage at the University of Georgia, Athens: proof (click link).

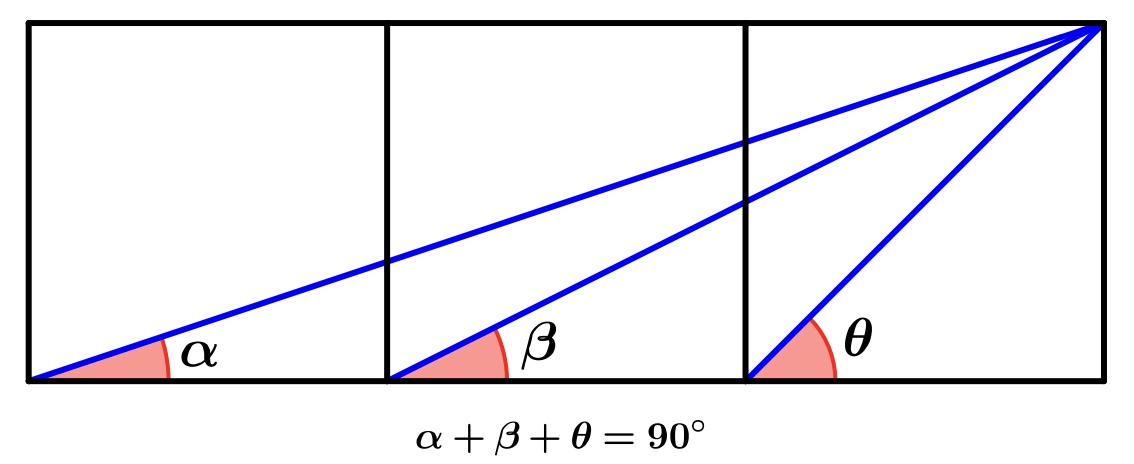
Application
This theorem and its converse has several useful applications in solving various different kinds of geometry problems. The so-called 'three squares' problem is just one such example:
Given three squares attached in a row as shown above, with the three diagonals drawn, prove that α + β + θ = 90°.

Note: A paper by Duncan Samson & Moshe Stupel about various solutions to the 'three squares' problem above, including using the converse of the Tangent-Secant Theorem, will be appearing in the December 2024 issue of the AMESA journal Learning & Teaching Mathematics.

External Links
Tangent–secant theorem
Tangent Secant Theorem
Converse of Tangent Secant Theorem
Power of a Point Theorem
Euclid Vol III, Proposition 37

**************
Free Download of Geometer's Sketchpad

**************

Back to "Dynamic Geometry Sketches"

Back to "Student Explorations"

Created by Michael de Villiers with WebSketchpad, 5 September 2024.