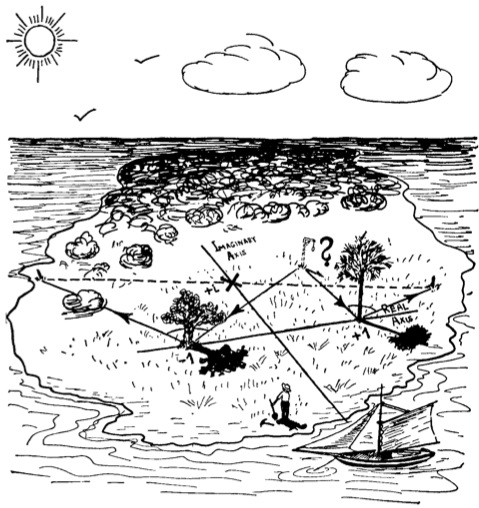

Pirate Treasure Hunt Problem
The picture above is from George Gamow's 1947 book One,
two three, infinity who was apparently the first to propose the following interesting 'pirate treasure hunt' problem:
"A man finds an old document left by his grandfather. The document gives specific directions for reaching a certain island. On this island, he has to locate a specific oak tree, a specific pine tree and a gallows. He is asked to start from the gallows and march up to the oak tree counting the number of steps needed to reach the oak tree. At the oak tree, he must turn to the right and march the same number of steps. At this spot he must put a spike in the ground. He must then return to the gallows and then march to the pine tree counting the number of steps needed to reach the pine tree. At the pine tree, he must now turn to the left and march the same number of steps. At the second spot he has to put another spike in the ground. He must then dig at the midpoint of the line segment connecting the two spikes to recover the treasure buried there. Upon reaching the island, the man easily finds the specific oak tree and the specific pine tree. However, much to his dismay, he cannot locate the gallows. Rain and decay completely obliterated any traces of the place where the gallows once stood. Can the man still find the treasure? If so, how?"
Pirate Treasure Hunt
Generalized Pirate Treasure Hunt
The treasure hunt problem above can be generalized using the
following transformation result: The sum of two spiral similarities (k,
a) and (1/k, b) around centres A and B
is a half-turn, if a + b = 180 degrees. (A spiral
similarity (k, a) around a point means an enlargement
with factor k followed by a rotation through angle a,
both with the same centre).
In the sketch above, click on the 'Link to Generalization' button to navigate to the above stated generalization.
Another Application
Alfinio Flores (1999) gives the following related result: Let ABC be any triangle, and choose any point D. Points Dl, D2, and D3 are obtained in the following way: Dl is the reflection of D around B, D2 is the reflection of Dl around A, and D3 is the reflection of D2 around C. Then the position of the midpoint M between D and D3 is fixed.
Reference: Flores, A. (1999). Mechanical Arguments in Geometry, PRIMUS, 9:3, 241-250, DOI: 10.1080/10511979908965930
In the sketch above, click on the 'Link to Another application' button to navigate to this related result.
Explaining (proving)
Can you explain why (prove) these three results are true? Can you
prove the results in different ways?
Hint
For a proof, try using this result: Sum of Rotations Theorem, or this equivalent one: Pompe's Hexagon Theorem.
Some References
a) Read my 2016 paper An explanatory, transformation geometry proof of a classic treasure-hunt problem and its generalization in the International Journal of Mathematical Education in Science and Technology.
(Note: This paper was based on talks given at the Annual Congress of the Association of Mathematics Education of South Africa (AMESA), 3–7 July 2000, University of Free State, Bloemfontein,
South Africa, as well as at the Annual Congress of the Mathematical Association (MA), 13–16
April 2004, University of York, United Kingdom.)
b) Read Gamow, G. (1947). One, Two, Three ... Infinity (12.5 MB). Dover Publications, New York, pp. 35-37.
c) Read David Dixon's (2006) coordinate proof of the original problem at Pirate Proof.
d) Read the two 2003 proofs of the original problem by David Lewine, a mathematics teacher attending some Dynamic Geometry workshops of Daniel Scher respectively at: i) First Proof - pdf and ii) Second Proof - Sketchpad 5 file.
Related Links
Finsler–Hadwiger theorem plus Gamow-Bottema's Invariant point
Sum of Two Rotations Theorem
Pompe's Hexagon Theorem
Van Aubel's Theorem and some Generalizations
Napoleon's Theorem: Generalizations & Converses
Back to "Dynamic Geometry Sketches"
Back to "Student Explorations"
Michael de Villiers, 2002; updated: 11 Sept 2010; 7 June 2016; 11 Nov 2016; 1 June 2022; 20 Nov 2023