De Villiers Points and De Villiers Hyperbola of a Triangle

Dual to Kosnita (De Villiers points of a triangle)

To my great surprise, I accidentally in August 2008 found out that these two special points of a triangle have been named after me at WolframMathWorld as the De Villiers Points in relation to a 1996 paper of mine in Mathematics & Informatics Quarterly (see below). They are referenced as Points 1127 and 1128 at the Encyclopedia of Triangle Centers. But one is immediately humbled (and also slightly bemused) by the fact that today (June 2022) there are more than 7 000 special points known in relation to the simple, elementary triangle, so mine are only two amongst thousands of other interesting ones!
Also note that I'd discovered the result below by formulating a dual in terms of incentres to correspond to the circumcentres of Kosnita's Theorem.

Dual to Kosnita (De Villiers points of a triangle)
1) If I is the incentre of triangle ABC, and the incenters D, E and F are respectively constructed for AIB, BIC and CIA, then the lines AE, BF and CD are concurrent in the inner (1st) De Villiers point DV1.
2) If K, L and M are the excentres of triangle ABC, and the incenters X, Y and Z are respectively constructed for AKB, BLC and CMA, then the lines AY, BZ and CX are concurrent in the outer (2nd) De Villiers point DV2.

Dual to Kosnita (De Villiers points)

Notes
1. For an easy proof of the concurrency, read my 1996 article A Dual To Kosnita's Theorem in Mathematics & Informatics Quarterly which uses a generalization of the Fermat-Torricelli theorem.
2. My more recent AMESA July 2009 paper From the Fermat points to the De Villiers points of a triangle more fully describes the discovery and proofs involved, tracing the origin from the Fermat points of a triangle.
3. My meer onlangse Sept 2010 artikel Vanaf die Fermat punte na die De Villiers punte van 'n driehoek beskryf die ontdekking en betrokke bewyse meer volledig, asook die oorsprong en ontwikkeling vanaf die Fermat punte van 'n driehoek.
4. I was pleasantly amused to recently find in an online paper in Aug 2015 by two Bulgarian mathematicians that they called the triangles DEF and XYZ the 'De Villiers' triangles, and proposed several conjectures, discovered by computer, of the (inner) De Villiers triangle in relation to the Malfatti-Steiner point. Read the paper at Grozdev Dekov paper (2015).

De Villiers Hyperbola
The three vertices of a triangle and the two De Villiers points lie on a hyperbola (click on the appropriate Link button in the above dynamic sketch, and then drag any of the three vertices of the triangle to see dynamically). Note that the illustrative diagram below is STATIC, and not dynamic.

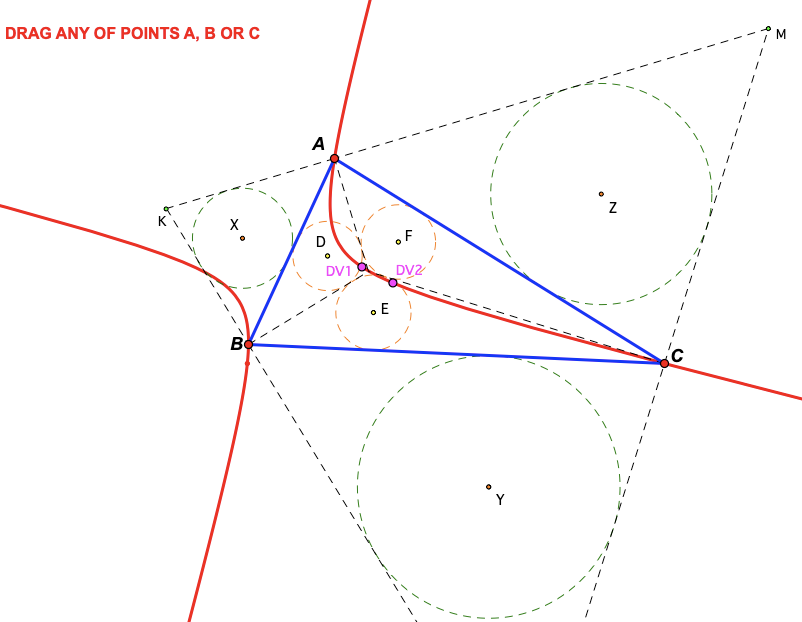
De Villiers Hyperbola

Obviously the 5 points (A, B, C, DV1 and DV2) are sufficient to determine a conic, but to prove that it is always a hyperbola relies on an interesting result proven by John Silvester, King's College, London, that a conic through the 3 vertices of a triangle, and a point that is always interior, is a hyperbola. For an unedited outline of his proof, go to Hyperbola Proof. It could perhaps be interesting to explore if there are other special triangle points that lie on this hyperbola, and with over 7000 special points, there is some chance that some of them may lie on it.

Collinearities
1) The first (inner) De Villiers point is collinear with points 174 and 481 in the Encyclopedia of Triangle Centers.
2) The second (outer) De Villiers point is respectively collinear with a) points 164 and 174, b) 188 and 519 as well as c) 258 and 505. Go to the Encyclopedia of Triangle Centers for definitions of these related points.

Some Further Investigations
1. Does the 1st De Villiers point exist in elliptic (spherical) geometry? Investigate using De Villiers point 1 - elliptic.
2. Does the 1st De Villiers point exist in hyperbolic geometry? Investigate using De Villiers point 1 - hyperbolic.
3. Does the 2nd De Villiers point exist in elliptic (spherical) geometry? Investigate using De Villiers point 2 - elliptic.
4. Does the 2nd De Villiers point exist in hyperbolic geometry? Investigate using De Villiers point 2 - hyperbolic.
5. The four non-Euclidean investigations above are best done with the free software Cinderella. Can you prove your observations?
6. What are the respective loci of the two De Villiers points if triangle ABC is inscribed in a given circle and BC is fixed so that only A moves along the circumference of the circle? Investigate by clicking on the appropriate Link button in the dynamic sketch at the top of this page.
7. Now ask some questions yourself and explore further!

360 ETC points
The following dynamic sketch displays the first 360 ETC points (click) listed at Clark Kimberling's Encyclopedia of Triangle Centers, plus the two De Villiers points.

External Links
X(1127) = 1st De Villiers Point
X(1128) = 2nd De Villiers Point
SA Mathematics Olympiad Questions and worked solutions for past South African Mathematics Olympiad papers can be found at this link.
(Note, however, that prospective users will need to register and log in to be able to view past papers and solutions.)

********************************
Free Download of Geometer's Sketchpad

********************************

Back to "Dynamic Geometry Sketches"

Back to "Student Explorations"

Created Michael de Villiers, 2009; modified 21 June 2016; updated to WebSketchpad, updated 9 July 2021; 28 June 2022; 3 Oct 2025.

Dual to Kosnita (De Villiers points of a triangle)

.sketch_canvas { border: medium solid lightgray; display: inline-block; } Dual to Kosnita (De Villiers points)

Dual to Kosnita (De Villiers points)