Fermat-Torricelli Point Generalization (Jacobi's Theorem) plus other further generalizations
Pierre de Fermat and Evariste Torricelli
Acknowledgement
I'm grateful to Dutch colleague, Floor van Lamoen, for bringing to my attention that the Fermat generalization given above is usually attributed to Karl Friedrich Andreas Jacobi (1795-1855). See p. 26 of his 1825 book Triangulorum Rectilineorum.
Some Historical Background & Learning Activities
In the special case (originally posed by Fermat in the 1600's and solved a little later by Torricelli) of the above result, when equilateral triangles are constructed on the sides of a triangle ABC (with none of its angles greater than 120 degrees), then the Fermat-Torricelli point, located at the point in the above sketch where DC, EA and FB meet, minimizes the sum of the distances from it to each of the vertices. More-over, for equilateral triangles constructed on the sides of the triangle, the line segments DC, EA and FB are equal - see for example, Mackay (1897).
A useful learning activity to illustrate to students the discovery function of proof is to let students start by exploring the concurrency of lines, and equality of the corresponding line segments, when equilateral triangles are constructed on the sides of a right triangle ABC rather than a general triangle. By explaining why the result is true, it then becomes obvious from the proof that the triangle need not be a right triangle, and therefore immediately generalizes to any triangle. This learning activity is now available in the free PDF download of my Rethinking Proof with Sketchpad book1.
One can also use the Fermat-Torricelli result for determining, for example, the optimal position for building an airport for 3 cities of more or less equal size. A learning activity, with a guided proof for students, is also available in the free PDF download of my Rethinking Proof with Sketchpad book1.
Note: 1(Information is provided inside the book on where to download the accompanying GSP sketches from).
The Fermat-Torricelli Generalization above is also of potential practical significance as it can be used to solve a 'weighted' airport problem, e.g. when the cities have populations of different size. For example, go to Weighted Airport Problem.
Published Paper
Download an article of mine from the Mathematical Gazette (1995) for a proof of the Jacobi theorem above from A generalization of the Fermat-Torricelli point. An earlier, different proof by Pargeter was also published in 1938 in the Mathematical Gazette.
Some Mathematical Applications
a) Jacobi's theorem easily provides a proof for the result of the so-called De Villiers Points of a Triangle as illustrated in the diagram below. (Click on the preceding Link to view a dynamic sketch).
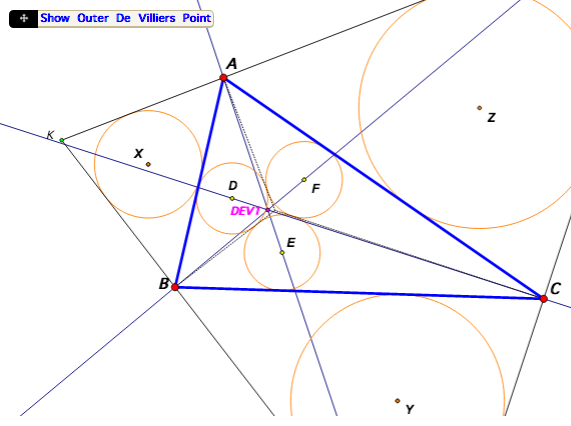
i) Click on the 'Show angles' button to display the measurements of angles ABD and ACF as well as the angle that AE makes with BC.
ii) Drag D and F until both angles ABD and ACF are approximately 90°. As shown in the (static) diagram below, what do you notice in regard to the angle that AE makes with BC?
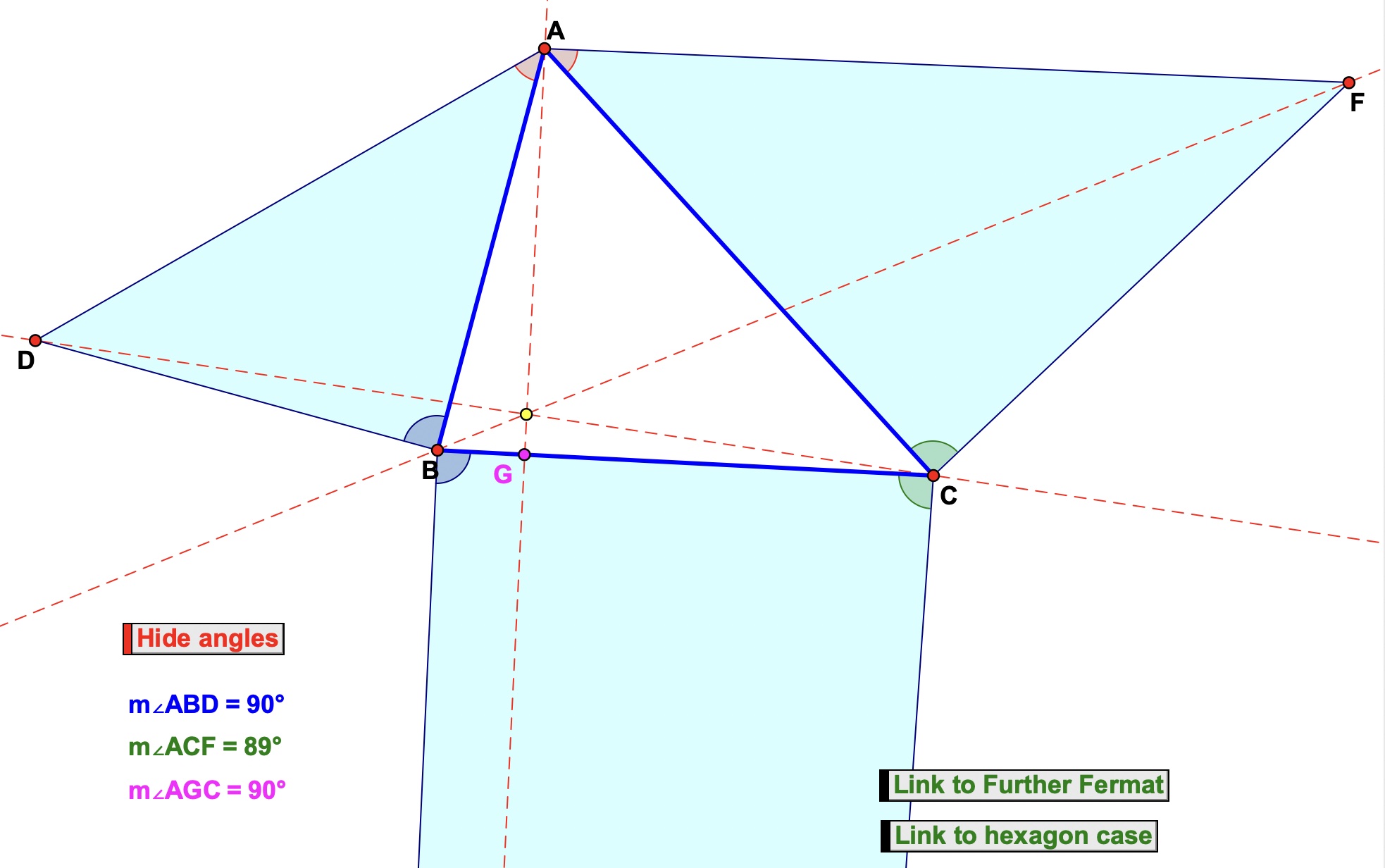
Further Fermat-Torricelli Generalization
If points K, L, M, N, O and P are constructed on the sides of triangle ABC so that BK/KC = CL/LB = CM/MA = AN/NC = AO/OB = BP/PA, triangles OPD, KLE and MNF are constructed so that ∠DOP = ∠FNM, ∠DPO = ∠EKL, ∠ELK = ∠FMN and triangles LMY, NOZ and PKX are respectively similar to triangles OPD, KLE and MNF, then DY, EZ and FX are concurrent.
2) Click on the link 'Further Fermat-Torricelli Generalization' button on the bottom right of the above sketch to navigate to a dynamic, interactive sketch illustrating this interesting, further generalization of Jacobi's theorem.
Comment: It is easy to see (and show) from the conditions of the Further Fermat-Torricelli point theorem above that BK = LC, CM = NA and AO = PB. More importantly, it follows that the opposite sides of the hexagon OPKLMN are parallel, and in the same ratio (e.g. ON/KL = PK/MN = LM/OP). Therefore, since the proof relies only on the underlying homothetic transformations, the concurrency result above applies to any hexagon of this type when similar triangles are constructed on opposite sides as before. This gives us the following useful corollary as an additional theorem.
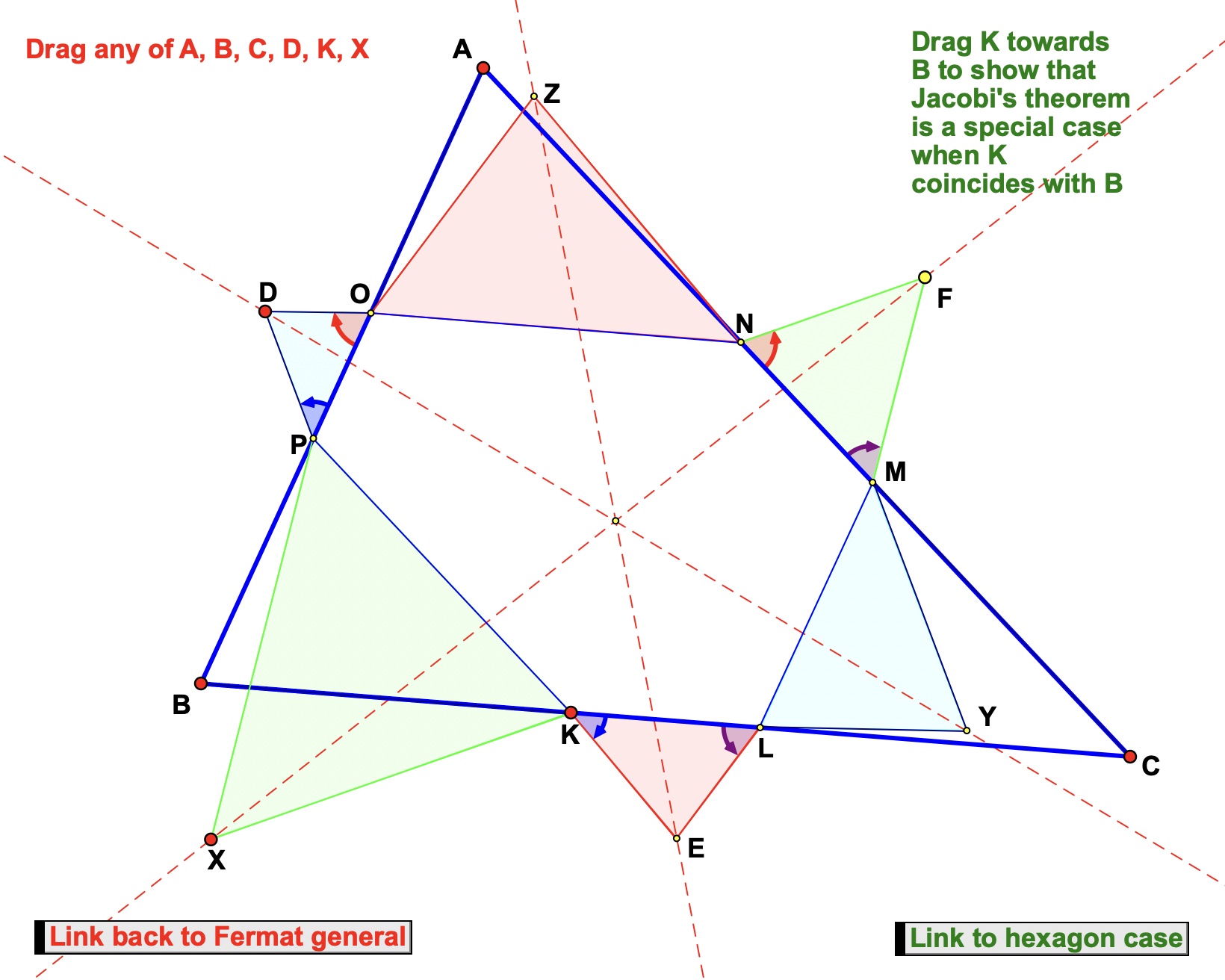
Hexagon Corollary
Given a hexagon ABCDEF with opposite sides parallel and in the same ratio (specifically FA/CD = DE/AB = BC/EF), and triangles ABG, CDH and EFI are constructed respectively similar to triangles DEK, FAL and BCJ so that ∠GAB = ∠IFE, ∠GBA = ∠HCD, ∠HDC = ∠IEF, (all six triangles constructed outwardly or inwardly), then LH, GK and JI are concurrent.
3) Click on the link 'hexagon case' button on the bottom right of the above sketch to navigate to a dynamic, interactive sketch illustrating this interesting corollary of the further Fermat-Torricelli generalization.
4) Explore the figure by dragging A, B, G or H as well as dragging E to change the ratio of the opposite sides.
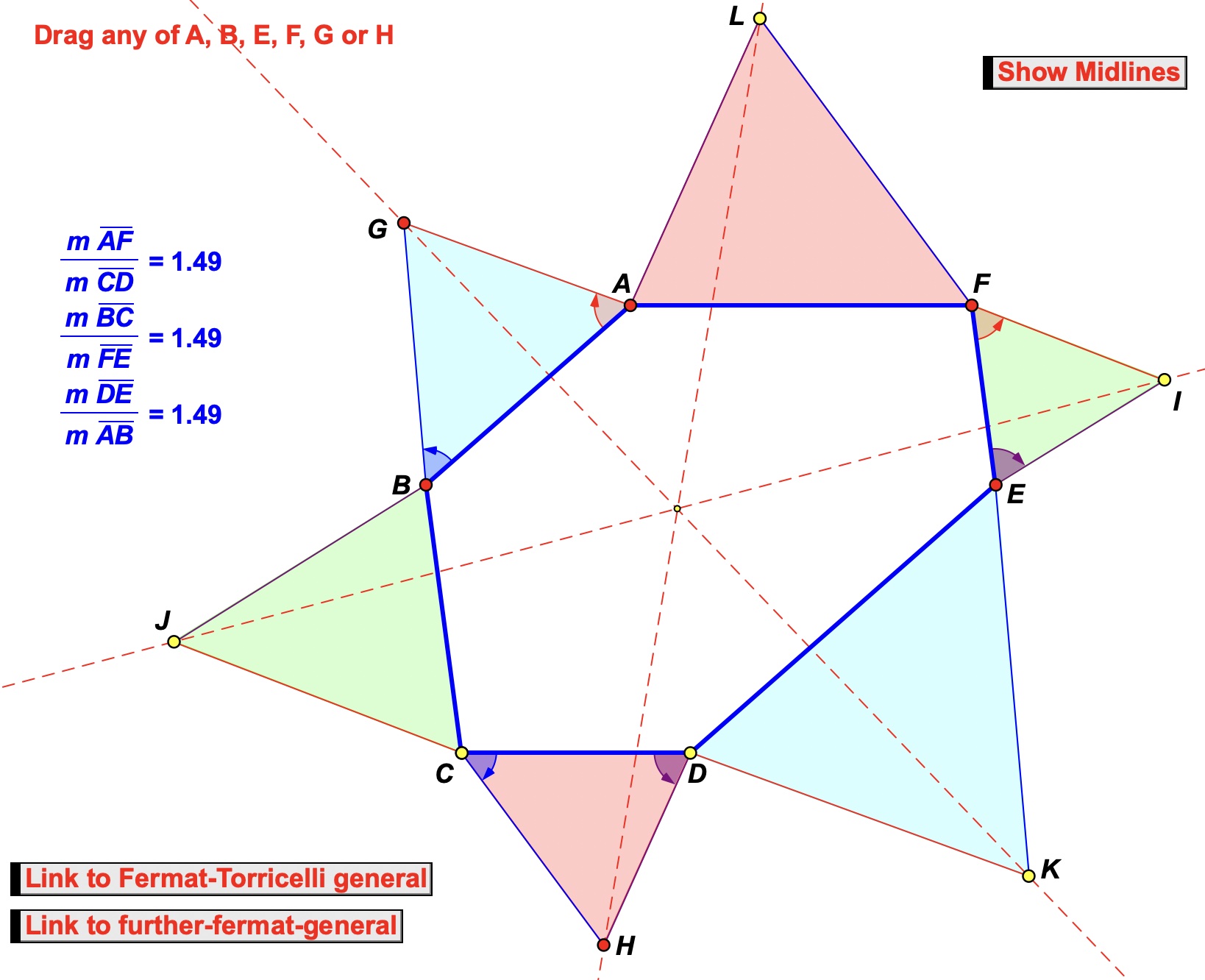
5) Next click on the 'Show Midlines' button to view the concurrency of the midlines, which is another related concurrency result from the Parallel-Hexagon Concurrency Theorem.
6) Drag G to the midpoint of AB and H to the midpoint of CD to see that for this particular type of hexagon the 'midlines concurrency result' can be viewed as a special case of this corollary.
7) However, note that the 'midlines concurrency' result is actually more general, since it is valid for any hexagon with opposite sides parallel. In contrast, the 'hexagon corollary' above does not generalize to any hexagon with opposite sides parallel, and a counter-example is not hard to find using dynamic geometry.
8) For another, different construction of a hexagon with opposite sides parallel and with opposite sides in the same ratio, click Using Dilation to construct a Parallel-hexagon with Opposite Sides in Same Ratio. This construction elegantly explains why a parallel-hexagon is obtained as well as why the concurrency is true.
......... 
(Note that the two images directly above are static. To access the dynamic versions of these sketches use the WebSketchpad sketch at the top.)
Published Paper
Download an article of mine from the Mathematical Gazette (1999) for a proof of the further generalization above from A further generalization of the Fermat-Torricelli point.
...........
Some Additional Notes
As mentioned earlier, an interesting property of the Fermat-Torricelli point that minimizes the sum of the distances to the 3 vertices of a triangle (with none of its angles > 120o) is that the three angles surrounding the optimal point are each equal to 120o. A physical model with 3 equal weights hung over pulleys, connected by thin rope, simulates the minimization of the distances, and moves to the optimal position when the system stabilizes. Pictures of such a simulation done with the assistance of Mahomed Bacus on the Edgewood Campus, UKZN are shown below.
Another beautiful way to illustrate the Fermat-Torricelli point is by using Soap Bubble Geometry. The physical properties of soap film are such that they would always tend to a shape or position of 'minimal energy'. It can therefore also be used to model solutions for the shortest road networks between 3, 4, 5, etc. cities (so-called Steiner networks). Some soap film solutions are illustrated at Minimal Soap Film 'Road' Networks from lectures at the Annual Meeting of the Mathematical Association. Below is an example of a physical soap bubble demonstration of a minimal path for a square that was often used by me in lectures at UKZN and at some AMESA conferences.
Lastly, a paper by Park & Flores explores the Fermat-Torricelli point from different perspectives, including an innovative kinematic method, which uses a constant relation between two vector functions to find a similar relation between the velocities of the corresponding endpoints of the vectors.
References
De Villiers, M. (1995). A generalization of the Fermat-Torricelli point. Mathematical Gazette, 79(485), pp. 374-378.
De Villiers, M. (1999). A further generalization of the Fermat-Torricelli point. Mathematical Gazette, (March), pp. 14-16.
De Villiers, (1999/2003/2012). Learning Activities (free downloads): The Fermat-Torricelli point (pp. 108-114) and Airport Problem (pp. 115-118) from Rethinking Proof with Sketchpad (free download), Key Curriculum Press, Emeryville.
Jacobi, K. F. A. (1825). Triangulorum Rectilineorum, p. 26.
Mackay, J.S. (1897). Isogonic Centres of a Triangle. Proc. Edinburgh Math. Soc. 15, pp. 100-118.
Park, J. & Flores, A. (2014). Fermat's point from five perspectives. International Journal of Mathematical Education in Science and Technology, DOI: 10.1080/0020739X.2014.979894.
Related Links
Bride's Chair Concurrency & Generalization
Weighted Airport Problem
De Villiers Points of a Triangle
Another concurrency related to the Fermat point of a triangle
Van Aubel's Theorem and some Generalizations
Another Construction of a Parallel-hexagon with Opposite Sides in Same Ratio
Napoleon's Theorem: Generalizations & Converses
Some Variations of Vecten configurations
Easy Hexagon Explorations
Parallel-Hexagon Concurrency Theorem
Toshio Seimiya Theorem: A Hexagon Concurrency result
A side trisection triangle concurrency
A 1999 British Mathematics Olympiad Problem and its dual
Concurrency, collinearity and other properties of a particular hexagon
Haag Hexagon and its generalization to a Haag Polygon
Haag Hexagon - Extra Properties
Conway’s Circle Theorem as special case of Side Divider Theorem
Some External Links
The Fermat Point and Generalizations
Fermat point
Jacobi's theorem (geometry)
**************
Free Download of Geometer's Sketchpad
...........