A Geometric Paradox Explained

A Geometric Paradox Explained
(Another variation of an IMTS problem)

"It doesn't matter how beautiful your theory is, it doesn't matter how smart you are. If it doesn't agree with experiment, it's wrong."
"The thing that doesn't fit is the thing that's the most interesting: the part that doesn't go according to what you expected."
- both quotes by Richard R. Feynman (1918-1988), famous American theoretical physicist & joint Nobel Prize in Physics winner in 1965

Problem
Note: the following curious, paradoxical geometry problem is yet another variation of an International Mathematical Talent Search (IMTS) problem available CLICK HERE.
"Determine the area of the crossed octagon ALBMCNDO as a fraction of the area of the square ABCD, where L, M, N, O are the midpoints of the sides of the square as indicated."

Explore
1) Click on the 'Show Areas' button below to view the two areas concerned. Drag any of the red vertices to explore.
2) What do you notice about the area of the crossed octagon ALBMCNDO in relation to that of the square? Do you find it surprising? Or perhaps even contradictory or confusing?
a) What is happening here? The situation looks quite paradoxical!
b) So the question is WHY does the software show the area of the crossed octagon equal to that of the square while the total area shaded in green is clearly less than that of the square?
c) Can the situation be explained & clarified?
3) Also note that the formed crossed octagon is not regular. However, it has all sides equal and alternate angles are equal as can be seen by clicking on the 'Show Side Lengths' and 'Show Angles' buttons. This crossed octagon is therefore what I've called a semi-regular side-gon, specifically in this case, a (crossed) 'semi-regular side-octagon' - which is a generalization to 2n-gons of the concept of a rhombus.

Area of crossed semi-regular side-octagon

Challenge
4) Paradox: Why is the area of the crossed octagon ALBMCNDO as calculated/determined by the software NOT equal to the total area of all the parts shown & shaded in 'green'by the software?
5) In order to correctly determine the area of a crossed polygon one has to use 'signed areas' as explained by Coxeter & Greitzer (1967). Using signed areas, can you explain why (prove that) the area of the crossed octagon ALBMCNDO equals the area of square ABCD as observed above? Can you explain (prove) it in more than one way?

Explanation & Proof
Click on the 'Link to proof' button above to navigate to a new sketch giving an explanation & proof by clicking on the 'Show Proof 1' and 'Show Proof 2' buttons.

Further Explanation
6) But why does the shaded representation in green of the crossed octagon ALBMCNDO by the software not agree with the proof above?
7) To further explain why it is a misleading representation, click on the 'Link to further-explanation1' button above to navigate to a new sketch & click on the buttons in the sketch. (Tip: If any of the buttons obscure some of the text, click on them & drag them into open space).
8) To continue in the same fashion as described in 7) above, click on the 'Link to further-explanation2' button above to navigate to a sketch showing the final overlay of all six triangles of which the crossed octagon ALBMCNDO is composed. What do you notice?
9) Click on the 'Link to Show Calculated Areas' button in 8) above to verify the final layering of the triangles.
10) What the above therefore shows is that while the area measurement of the area of the crossed octagon ALBMCNDO is correct, its shaded representation by the dynamic geometry software can be quite misleading as in this case. It is understandable though that programming the software to consistently be able in various crossed configurations to not only 'display' the kind of 'layering' shown in steps 8) and 9), but also to correctly count the overlays, would be quite challenging. Similar representation issues for a crossed hexagon appear in Inscribed Polygons. However, it is not a problem as long as users are aware of the shortcomings of the shaded representations of crossed polygons.

Other Software
Other dynamic geometry software have similar issues when dealing with representing crossed polygons, though all of them correctly measure/determine the area of the crossed octagon above. GeoGebra, for example, gives exactly the same representation as Sketchpad for the crossed octagon AGBHCEDF. Geometry Expressions also displays it in the same way with 'holes', but as shown in the first picture below, also provides a formal, symbolic solution in terms of the side length a as shown in the first picture below.
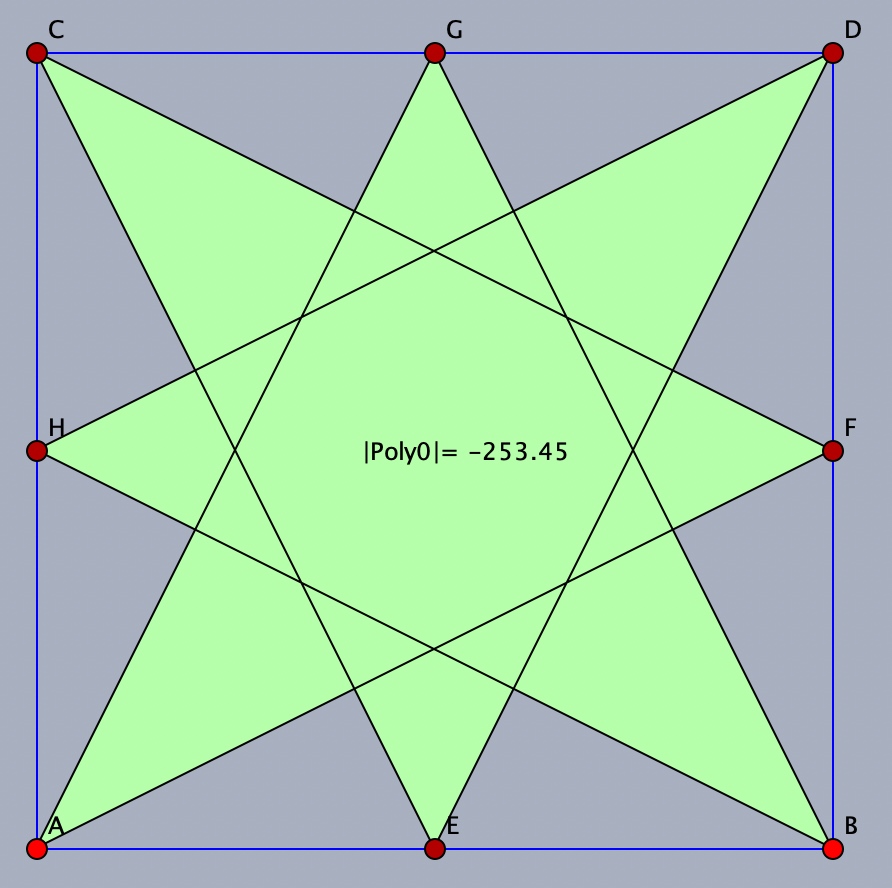
However, Cinderella as shown in the second picture below, provides a more accurate representation than the other three software of the crossed octagon by showing the shading without the eight 'holes'. But it still does not show the number of overlays of the various triangles (as in steps 8) and 9) above). Cinderella also more correctly uses signed areas, giving the area of the crossed octagon AGBHDECF as negative since its vertices are orientated in a clock-wise fashion.

........

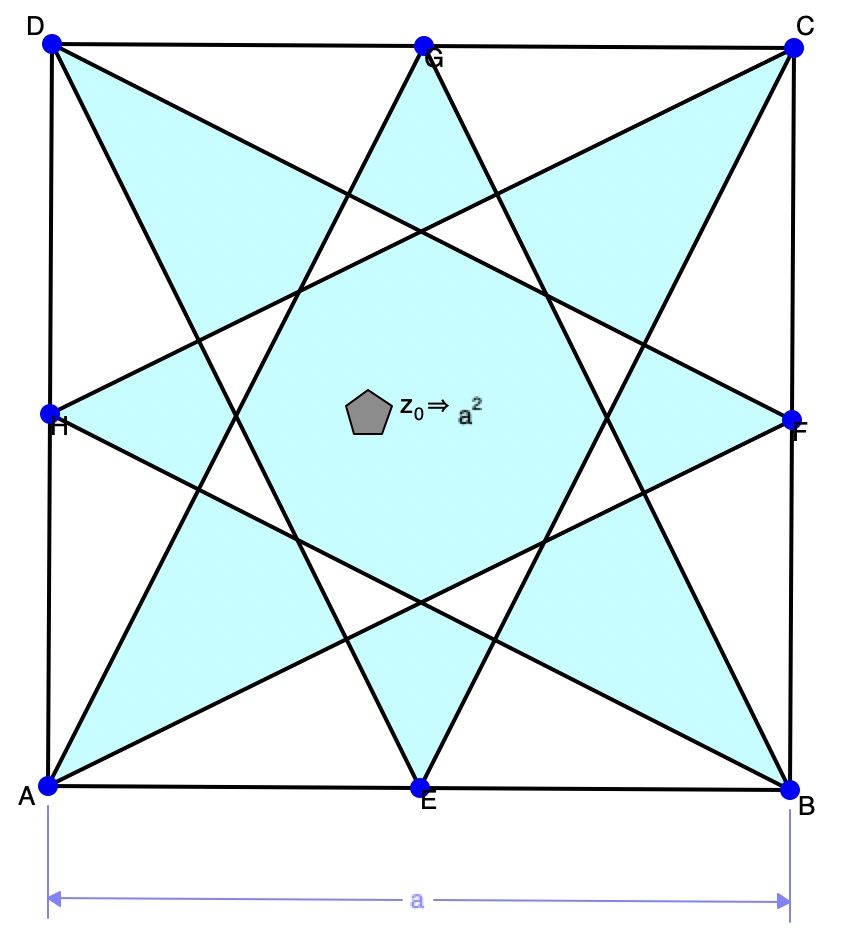Submitted Paper
A paper on this topic entitled "A Geometry Puzzler and its Explanation" will in due course be submitted to the Learning & Teaching Mathematics journal.

References
Coxeter, H. S. M. & Greitzer, S. L. (1967). Geometry Revisited. MAA, Washington, pp. 51-54.
De Villiers, M. (1994/2009). Some Adventures in Euclidean Geometry. Morrisville, NC: Lulu Publishers.
De Villiers, M. (1998). A Sketchpad discovery involving triangles and quadrilaterals. KZN Mathematics Journal, 3(1), 18-21.
De Villiers, M. (2014). Slaying a Geometrical Monster: Finding the Area of a Crossed Quadrilateral. Scottish Mathematical Council Journal, 44 (Dec), pp. 71-74.
De Villiers, M. (2015). I have a dream: Crossed Quadrilaterals - a Missed Lakatosian Opportunity?. Philosophy of Mathematics Education Journal, No. 29, July.
De Villiers, M. (2020). The Value of using Signed Quantities in Geometry. Learning and Teaching Mathematics, No. 29, pp. 30-34.

Free Download of Geometer's Sketchpad

***********

Back to "Dynamic Geometry Sketches"

Back to "Student Explorations"

Created by Michael de Villiers with WebSketchpad, 9 Oct 2023; updated 4 March 2024.