The famous concept of a 'golden rectangle' - a rectangle with its sides in the the golden ratio φ = (√5 + 1)/2 - dates back to ancient Greece & other civilizations. The concept can be extended to those of 'golden quadrilaterals' in several different ways as shown below (De Villiers, 2017).
Contrary to popular belief, definitions in mathematics are somewhat arbitrary & often a matter of choice & convenience. Sometimes definitions for mathematical objects are only formulated after the objects have been known & studied for some time - this is 'a posteriori' (descriptive) defining. Other times mathematical objects are preceded & defined into being by prior definitions - this is 'a priori' (constructive) defining - and only afterwards their properties are studied more extensively (De Villiers, 1986).
Since most of the 'golden quadrilaterals' below do not necessarily already have fixed, agreed-upon definitions, nor have their properties been studied extensively, the activity on this webpage provides a genuine opportunity at an elementary level to illustrate the mathematical process of 'constructive defining' (De Villiers, 1998). Seeing, for example, that a mathematical concept like a 'golden parallelogram' can be conceptualized & defined in different ways can be an important eye-opening educational experience regarding the 'propositional' nature of mathematics.
For example, if we choose to define a 'golden parallelogram' in a particular way, then we can derive & deduce certain properties from it as a consequence. But defining it in another, different way will lead to the derivation & deduction of other different properties. So just as different axioms determine different geometries or algebras, so will choosing different possible definitions for the golden quadrilaterals below, determine different concepts in each case, each with different properties.
Explore: Click on the names or the picture icons below to open an Exploration of each of the four given golden quadrilaterals, using dynamic geometry sketches created with WebSketchpad. Each Exploration has some Challenges for the reader, ranging from very easy to medium hard. Enjoy!
Explorations
Critical Comparison
5) The reader is invited to critically compare the possible definitions of each of the golden quadrilaterals above, judging them not only by 'appearance', but also by their mathematical properties & the ease by which one can construct an example or deduce other additional properties (not contained in the definition).
Try Some Defining Yourself
6) Can you think of possible ways to define a 'golden trapezium (trapezoid)'? Compare your constructive definitions with the classroom notes of John Olive (undated).
7) Can you think of possible ways to define a 'golden cyclic quadrilateral' that involves the golden ratio (but is not a golden rectangle)?
(Though perhaps not particularly 'visually appealing', one possibility might be a 'cyclic Kepler quadrilateral' (De Villiers, 2018), which is a cyclic quadrilateral with its sides in geometric progression with common ratio √φ).
8) Can you think of possible ways to define a 'golden hexagon', 'golden septagon', 'golden octagon', etc.?
9) One can also explore φ proportions in the angles of quadrilaterals as Fonseca (2021) has done, and which he has named 'phiangular quadrilaterals'. It is left to the reader to explore this approach further.
Precious Metal Ratios
It is often claimed that there is some inherent aesthetic preference to the golden ratio in art, architecture and nature. However, several recent psychological studies on peoples’ preferred choices from a selection of differently shaped rectangles, triangles, etc., do not show any clear preference for the golden ratio over other ratios (e.g., see Grossman et al, 2009; Stieger & Swami, 2015). Such a finding is hardly surprising since it seems very unlikely that one could easily visually distinguish between a rectangle with sides in the golden ratio 1.618, or say with sides in the ratio of 1.6, 1.55 or 1.65, or even from those with sides in the ratio 1.5 or 1.7.
It is well-known that the ratio of successive terms of the Fibonacci sequence tend towards the golden ratio. However, as mentioned in De Villiers (2009), it's quite easy to define a general recurrence relationship Fn + Fn+k = Fn+k+1 in which the ratio of successive terms converge to different limits for k = 0, 1, 2, ... (with k = 1 giving us the familiar Fibonacci sequence). These limits can be called the 'precious metal ratios' and the corresponding rectangles can be called the platinum, gold, silver, bronze, etc. rectangles. Examples of corresponding 'precious metal' rectangles for k = 0, k = 1 and k = 2, with the ratio of the sides a/b respectively equal to 2, 1.62 (rounded off to 2 decimals) and 1.47 (rounded off to 2 decimals), are shown below. Each example shows a square cut off from the left. It is also obvious that as k increases, b approaches a and the rectangle tends more and more towards a square.
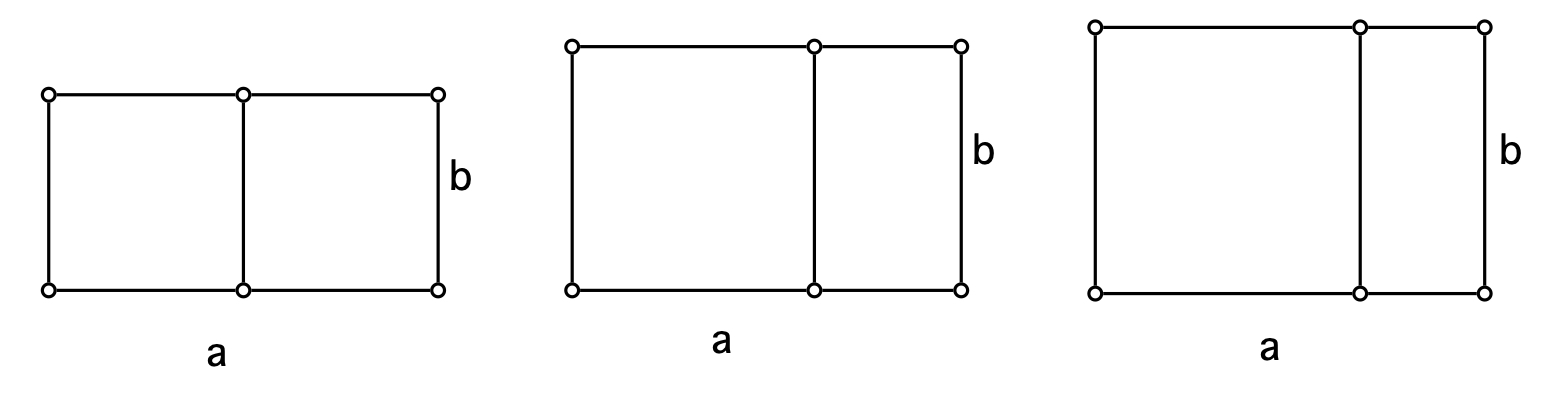
Lastly, it is left to the reader to possibly consider constructively defining 'precious metal' quadrilaterals as we have seen above with some examples of possible 'golden quadrilaterals'.
...............
References
De Villiers, M. (1986). The Role of Axiomatisation in Mathematics and Mathematics Teaching. University of Stellenbosch: Research Unit for Mathematics Education.
De Villiers, M. (1998). To Teach Definitions in Geometry or Teach to Define?. In A. Olivier & K. Newstead (Eds), Proceedings of the Twenty-second International Conference for the Psychology of Mathematics Education, Vol. 2, pp. 248-255, University of Stellenbosch: Stellenbosch, 12-17 July 1998.
De Villiers, M. (2009). Generalizing the Golden Ratio and Fibonacci. Learning & Teaching Mathematics, No. 7, pp. 39-41.
De Villiers, M. (2017). An Example of Constructive Defining: From a Golden Rectangle to Golden Quadrilaterals. At Right Angles, Vol. 6, No. 1 (March), Part 1, pp. 64-69; Vol. 6, No. 2 (August), Part 2, pp. 74-81.
De Villiers, M. (2018). A Cyclic Kepler Quadrilateral and the Golden Ratio. At Right Angles, Vol. 7, No. 1 (March), pp. 91-94.
Fonseca, J. (2021). Introducing A New Golden Triangle, Golden Quadrilaterals, a Golden Irregular Pentagon and Other Phigons. Published online at ResearchGate.
Grossman, P. et al. (2009). Do People Prefer Irrational Ratios? A New Look at the Golden Section. Student research conducted in 2008/2009 in the Dept. of Applied Computer Science, University of Bamberg.
Olive, J. (Undated). Classroom Notes: Construction and Investigations of Golden Trapezoids. Downloaded from University of Georgia (Athens), USA on 23 Oct 2016.
Stieger, S. & Swami, V. (2015). Time to let go? No automatic aesthetic preference for the golden ratio in art pictures. Psychology of Aesthetics, Creativity, and the Arts, Vol 9(1), Feb, 91-100.
Related Links
Similar Parallelograms: A Generalization of a Golden Rectangle property
Cyclic Kepler Quadrilateral Conjectures
Golden Ratio Parallel-hexagon
A diagonal property of a Rhombus constructed from a Rectangle
A Fibonacci Generalization - Kendal's theorem
Some External Links
Bartlett, C. (2019). Nautilus Spirals and the Meta-Golden Ratio Chi. Nexus Network Journal, 21:641–656.
'Golden Rectangle'
Golden Ratio (Wikipedia)
Golden Ratio (Cut the Knot)
Fibonacci sequence
Myth-busting the Golden Ratio
The Parthenon and the Golden Ratio: Myth or Misinformation?
The Golden Ratio: Design’s Biggest Myth
Back to "Dynamic Geometry Sketches"
Back to "Student Explorations"
Created by Michael de Villiers, 24 February 2022; updated 22 Nov; 15 Dec 2023.
