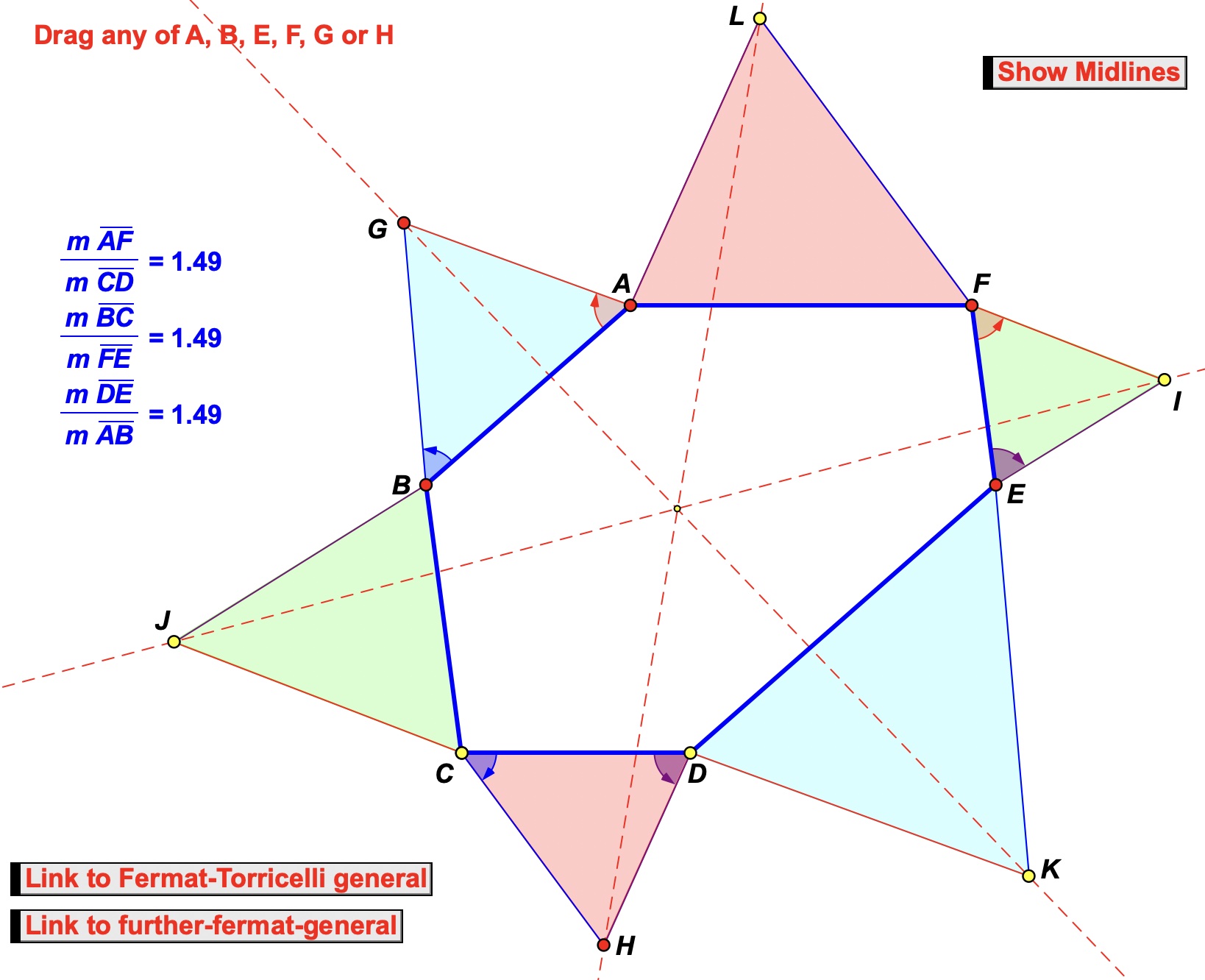
The following corollary involving a parallel-hexagon (a hexagon with opposite sides parallel) is given in Fermat-Torricelli Point Generalization (aka Jacobi's theorem) (see De Villiers, 1999), namely:
Given a parallel-hexagon ABCDEF with opposite sides in the same ratio (specifically FA/CD = DE/AB = BC/EF), and triangles ABG, CDH and EFI are constructed respectively similar to triangles DEK, FAL and BCJ so that ∠GAB = ∠IFE, ∠GBA = ∠HCD, ∠HDC = ∠IEF, (all six triangles constructed outwardly or inwardly), then LH, GK and JI are concurrent.
The construction below immediately provides an explanatory proof of the corollary.

(Note that the image directly above is static. To access a dynamic version of this sketches follow the 'Fermat-Torriceli' link given at the top, and navigate to the 3rd sketch using the given buttons in the displayed sketch.)
Another Construction of a Parallel-hexagon with Opposite Sides in Same Ratio
The following, different construction (see dynamic figure below) also produces a parallel-hexagon with opposite sides in the same ratio (and can be viewed as equivalent to the one given in the link above):
1) Start with an arbitrary △PQR, and dilate all three its sides, in both directions from each of the endpoints, with the same scalar factor a.
2) Label the images of the above dilations as shown below.
3) Click on the 'Show Ratios Opposite Sides' and the 'Show Diagonal Ratios' buttons. What do you notice?
4) Drag the slider point a to change the scale factor (or any of the other red vertices). What do you notice? Can you explain/prove your observations?
For this differently constructed parallel-hexagon we now also obtain the same concurrency result as the one mentioned at the top.
Parallel-hexagon Concurrency Theorem
Given a parallel-hexagon ABCDEF with opposite sides in the same ratio (specifically AB/DE = CD/FA = EF/BC), and triangles ABG, CDH and EFI are constructed respectively similar to triangles DEK, FAL and BCJ so that ∠GAB = ∠IFE, ∠GBA = ∠HCD, ∠HDC = ∠IEF, (all six triangles constructed outwardly or inwardly), then LH, GK and JI are concurrent.
Explanatory Proof
This simple construction not only explains why the obtained hexagon has opposite sides parallel, and in the same ratio, but also if we reverse the above transformation (from hexagon back to triangle), it's quite obvious that it simple reduces the result to Jacobi's theorem in relation to △PQR. The beauty of this construction, therefore, is in its simplicity as well as its explanatory power.
Another Parallel-hexagon with Opposite Sides in Same Ratio
Golden Ratio Parallel-hexagon
If we choose the scale factor to create this parallel-hexagon equal to the golden ratio φ = (√5 + 1)/2, we obviously will have the opposite sides in the ratio φ + 1 while the diagonals are divided into the ratio φ.
5) Click on the link 'golden ratio parallel-hexagon' button on the bottom right of the above sketch to navigate to a new dynamic, interactive sketch illustrating the above properties.
Some Additional Notes
The construction of the parallel-hexagon above generalizes Odom's construction which starts with an equilateral triangle instead of an abitrary triangle. Starting with an equilateral triangle, however, produces a semi-regular angle-hexagon - a cyclic hexagon with all angles equal and two sets of alternate sides equal (De Villiers, 2011; De Villiers, 2017, p. 80). More interesting properties of "Odom's Triangle" have been further investigated by Hung & van Lamoen (2021) and is recommended further reading.
References
De Villiers, M. (1999). A further generalization of the Fermat-Torricelli point. Mathematical Gazette, (March), pp. 14-16.
De Villiers, M. (2011). Equi-angled cyclic and equilateral circumscribed polygons. The Mathematical Gazette, 95(532), pp. 102-106.
De Villiers, M. (2011). Feedback: Equi-angular cyclic and equilateral circumscribed polygons. The Mathematical Gazette, 95(533), p. 361.
De Villiers, M. (2017). An Example of Constructive Defining: From a Golden Rectangle to Golden Quadrilaterals. At Right Angles, Vol. 6, No. 1 (March), Part 1, pp. 64-69; Vol. 6, No. 2 (August), Part 2, pp. 74-81.
Hung, T.Q. & van Lamoen, F. (2021). Odom’s Triangle. International Journal of Computer Discovered Mathematics (IJCDM), Volume 6, 2021, pp. 68-77.
Related Links
Fermat-Torricelli Point Generalization (aka Jacobi's theorem)
Semi-regular Angle-gons and Side-gons: Generalizations of rectangles and rhombi
Golden Quadrilaterals (Generalizing the concept of a golden rectangle)
Cyclic Kepler Quadrilateral & the Golden Ratio
The Parallel-pentagon and the Golden Ratio
Easy Hexagon Explorations
Parallel-Hexagon Concurrency Theorem
Toshio Seimiya Theorem: A Hexagon Concurrency result
A side trisection triangle concurrency
A 1999 British Mathematics Olympiad Problem and its dual
Concurrency, collinearity and other properties of a particular hexagon
Haag Hexagon and its generalization to a Haag Polygon
Haag Hexagon - Extra Properties
Conway’s Circle Theorem as special case of Side Divider Theorem
Some External Links
Hexagons and the Golden Ratio
...........