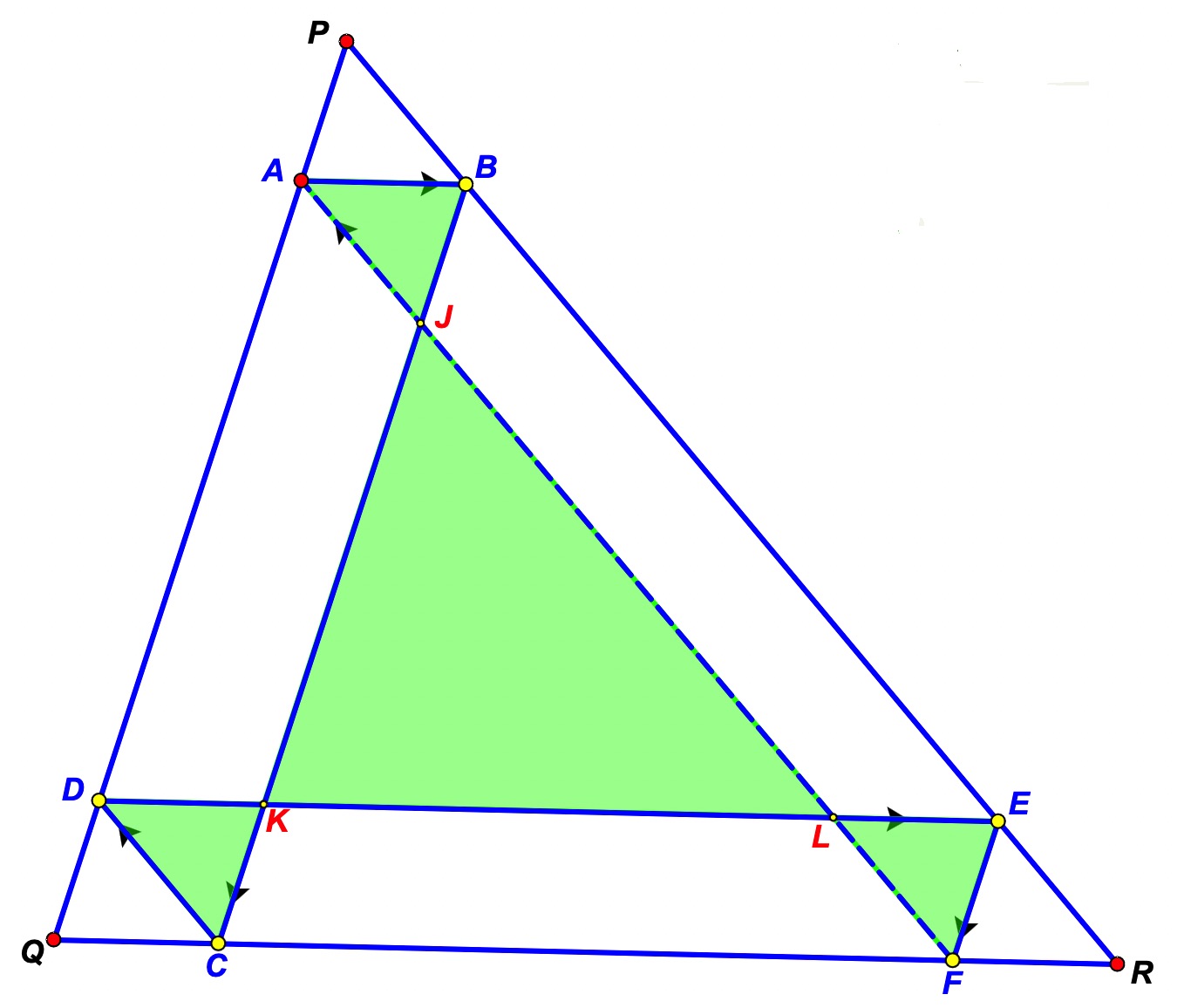
As explored at Another generalization of Varignon's theorem (click on the 'Link to Triangle' button): if we start from any point on the side of a triangle & continue drawing parallel lines to the sides as shown below, we end up with a closed, crossed hexagon.

But drawing lines parallel to the sides of a triangle is equivalent to drawing lines parallel to the sides of the medial (or midpoint) triangle, which is formed by the medians of the triangle. So what happens if instead we consider lines drawn parallel to the sides of a cevian triangle formed by three concurrent cevians?
Investigate
Given a triangle ABC, with 3 cevians AD, BE and CF concurrent at P. Choose an arbitrary point G on AB. Draw a line GH parallel to FE to intersect AC at H. Continuing from H draw a line HI parallel to ED, etc. Click on the red buttons on the left to draw these lines in order.
Merry Go Round the Triangle
Conjecture
What do you notice? What conjecture(s) can you make?
When will the centre Q of the conic coincide with P?
Explore further by dragging any of the red vertices (except P).
Challenge
Can you prove your conjecture(s) above?
Published Paper
Read our joint article (together with John Silvester) "A Merry-Go-Round the Triangle" published in the June 2018 issue of the Learning and Teaching Mathematics journal of AMESA.
Related Links
Area ratios of some parallel-polygons inscribed in quadrilaterals and triangles
Nine Point Conic and Generalization of Euler Line
Spieker Conic and generalization of Nagel line
Six Point Cevian Circle
Parallel-Hexagon Concurrency Theorem
Toshio Seimiya Theorem: A Hexagon Concurrency result
Conway's Circle Theorem as special case of Side Divider (Windscreen Wiper) Theorem
A side trisection triangle concurrency
British Mathematical Olympiad problem: Conic Generalization
Eight Point Conic for Cyclic Quadrilateral
Rigby's Eight Point Conic for a Quadrilateral
Conic by half-turn
Experimentally Finding the Centroid of a Triangle with Different Weights at the Vertices
Free Download of Geometer's Sketchpad
***********
Back to "Dynamic Geometry Sketches"
Back to "Student Explorations"
Michael de Villiers, created 21 March 2018; updated 3 July 2018; 9 April 2024.