Related Variations & Generalizations of Napoleon's Theorem

Napoleon Related Variation 1: If similar triangles ABD, EBC and AFC are erected on the sides of any triangle ABC, and G, H and I are incentres of these triangles, then they form a triangle so that ∠G = ½(∠DAB + ∠DBA), ∠H = ½(∠EBC + ∠ECB) and ∠I = ½(∠FCA + ∠FAC).

Napoleon Related Variation 1 (1995)

*****

Napoleon Related Variation 2: If triangles AGB, HCB and IAC are erected on the sides of any ΔABC, so that ∠GAB = ∠HCB = α, ∠HBC = ∠IAC = β and ∠ICA = ∠GBA = γ and α + β + γ = 90^o, then ∠HGI = 2β, ∠GHI = 2γ and ∠GIH = 2α.

Important: To view & manipulate the dynamic version of this 2nd generalization, navigate to it using the appropriate button in the ABOVE dynamic sketch; the picture below is static.

Napoleon Related Variation 2 (1995)

Note:
1) If in the hexagon AGBHCI above, AG = AI, BG = BH and CH = CI (or GA = GB, HB = HC and IC = IA), we obtain a configuration meeting the conditions of Pompe's Hexagon Theorem (2016).
2) It can also be used to solve/prove this interesting Dirk Laurie Tribute Problem.

*****

Special Case of Napoleon Related Variation 2: If similar, acute-angled triangles DBA, CBE and CFA are erected on the sides of any triangle ABC, then the orthocentres of the three triangles form a triangle with ∠HGI = 2∠HBC, ∠GHI = 2∠ICA and ∠GIH = 2∠GAB.

Important: To view & manipulate the dynamic version of this 2nd generalization, navigate to it using the appropriate button in the dynamic sketch right at the TOP; the picture below is static.

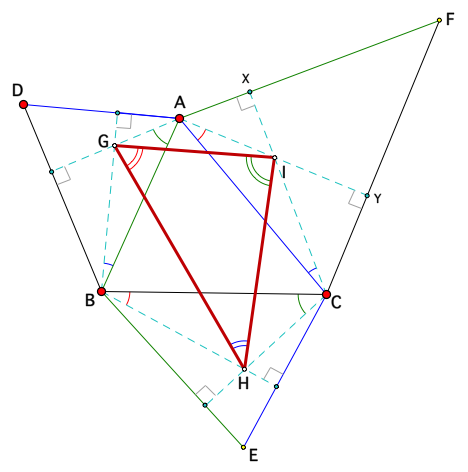
Special Case of Napoleon Related Variation 2

*****

Napoleon Related Variation 3 - Michael Fox's Theorem: If similar triangles DBA, CBE and CFA are erected on the sides of any triangle ABC, and points G, H and I are in the same relative positions in these triangles, then ∠HGI = ∠HBC + ∠IAC, ∠GHI = ∠ICA + ∠GBA, and ∠GIH = ∠GAB + ∠HCB.

Important: To view & manipulate the dynamic version of this 2nd generalization, navigate to it using the appropriate button in the dynamic sketch right at the TOP; the picture below is static.

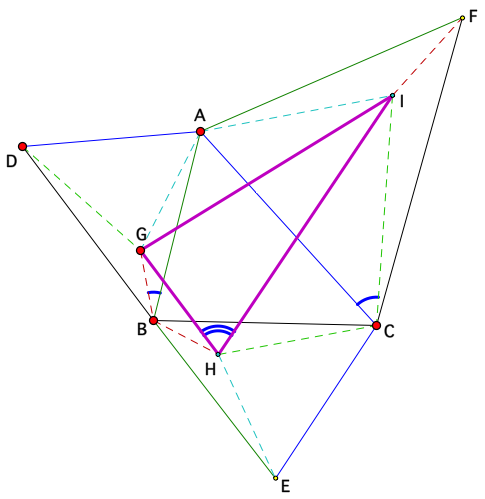
Napoleon Related Variation 3 - Michael Fox's Theorem (1998)

References
i) De Villiers, M. & Meyer, J. (1995). A generalized dual of Napoleon's theorem and some further extensions. Int. J. Math. Ed. Sci. Technol., 26(2), pp. 233-241.
ii) De Villiers, M. (1996). Some Adventures in Euclidean Geometry, pp. 179-180.
iii) Fox, M. (1998). Napoleon triangles and adventitious angles. The Mathematical Gazette, Nov., pp. 413-415.

Egamberganov's Theorem: In a 2017 paper A generalization of the Napoleon's Theorem in Mathematical Reflections, no. 3, Khakimboy Egamberganov generalizes Napoleon's Theorem even further, and applies it to solve several interesting Olympiad type problems, including Pompe's Hexagon Theorem. The beauty of Egamberganov's Theorem is that it's also a generalization of all four the results above. His theorem can be seen as a hexagon theorem and can be formulated as follows in relation to the four sketches above:

Given a hexagon AGBHCI with AG* BH * CI = GB * HC * IA, and ∠AGB + ∠BHC + ∠CIA = 360^o, then ∠HGI = ∠HBC + ∠IAC, ∠GHI = ∠ICA + ∠GBA, and ∠GIH = ∠GAB + ∠HCB. (A dynamic geometry sketch of this theorem will be done in due course & posted in the next update).

Related Links
Some Circle Concurrency Theorems
Pompe's Hexagon Theorem
Bride's Chair Concurrency & Generalization
A variation of Miquel's theorem and its generalization
Fermat-Torricelli Point Generalizations
Weighted Airport Problem
Some Variations of Vecten configurations
Dirk Laurie Tribute Problem
Another concurrency related to the Fermat point of a triangle plus related results
Anghel's Hexagon Concurrency theorem

Free Download of Geometer's Sketchpad