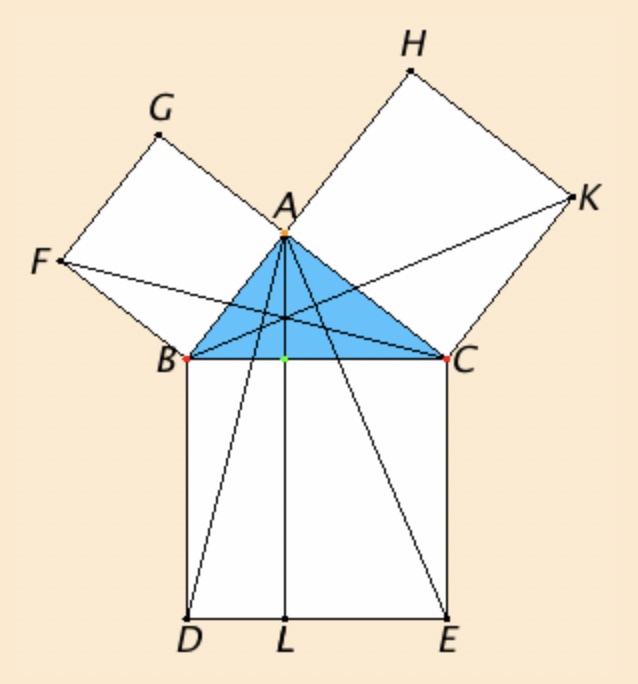

The above diagram appears in the classic "Bride's Chair", "Windmill", "Tail of the Peacock" diagram of Euclid's 300 BC proof of the Theorem of Pythagoras - see for example Euclid's Elements, Book 1, Proposition 47. As can be seen, the lines BK and CF are concurrent with the perpendicular from A to BC. However, it is not stated or proven in Euclid's Elements.
General Theorem
The triangle, however, doesn't have to be right-angled for the concurrency to hold, but can be any triangle as shown in the dynamic sketch below, and the general theorem can be stated as follows:
Given any triangle ABC with squares ABFG, BCED and CAHK constructed on the sides, then CF, BK, and the altitude from A to BC are concurrent in M.
Explore: Drag any of the red vertices A, B or C to dynamically explore the diagram.
Bride's Chair Concurrency & Generalization
Challenge
1) Can you explain why (prove that) the result is true?
2) Can you explain (prove) it in more than one way?
Brief Historical Background
a) Heron or Hero (c. 10-70 AD) of Alexandria gave a proof of this concurrency result making use of 3 lemmas and basing his proof entirely on Book 1 of Euclid's Elements (see Hawking, 2005).
b) A French mathematician by the name of Vecten in the early 1800's extensively studied the configuration of an arbitrary triangle with squares on the sides, including apparently proving the general concurrency above (XYZ, 2008).
c) Coxeter & Greitzer (1967) gives the concurrency problem as an exercise on p. 84-85, and a proof using Ceva's theorem on p. 169.
d) A more thorough historical overview is given by XYZ (2008) as well as a proof using similarity.
e) The Bride's Chair concurrency can also be viewed as a special limiting case of Jacobi's Theorem - click on the link for more details.
Explore More
3) Click on the 'Link to squares locus' button to navigate to a new sketch, then drag A along the circumcircle of triangle ABC.
4) What do you notice about the locus (path) of M as A is moved along the circumcircle in 3)? What is the locus of M? Can you explain/prove your observations?
5) All squares are similar. What happens if other similar quadrilaterals are placed on the sides? Does the concurrency still hold?
6) Click on the 'Link to similar rectangles' button to navigate to a new sketch.
7) What do you notice? Drag any of the vertices A, B or C. Can you explain/prove your observations?
8) Click on the 'Link to similar rectangles locus' button to navigate to a new sketch, then drag A along the circumcircle of triangle ABC.
9) What do you notice about the locus (path) of M as A is moved along the circumcircle in 8)? What is the locus of M? Can you explain/prove your observations?
10) Explore other similar quadrilaterals, and arrangements, on the sides of ABC on your own using dynamic geometry software.
References
Coxeter, H.S.M. & Greitzer, S.L. (1967). Geometry Revisited. Washington: Mathematical Association, pp. 84-85, p. 169.
Hawking, S. (Ed.) (2005). God created the integers: Mathematical breakthroughs that changed history. London: Penguin Books, pp. 23-24.
XYZ. (2008). Euclid’s Ever-turning Windmill. Unpublished personal communication by a colleague who prefers to remain anonymous.
Related Links
Napoleon's Theorem: Generalizations & Converses
Van Aubel's Theorem and some Generalizations
Finsler–Hadwiger theorem plus Gamow-Bottema's Invariant point
A Fundamental Theorem of Similarity
An associated result of the Van Aubel configuration and some generalizations
A Vecten area variation (Cross's theorem) & generalizations to quadrilaterals
Some Variations of Vecten configurations
Fermat-Torricelli Point Generalization (aka Jacobi's theorem) plus Further Generalizations
Euclid 1-43 Parallelogram Area Theorem
Some External Links
Euclid's Elements
Bride's Chair (Cut the Knot)
Bride's Chair (Wikipedia)
Vecten points
Finsler–Hadwiger theorem
Outer Vecten Triangle
...........