Some Triangle Generalizations of Napoleon's Theorem

Generalization 1
If similar triangles DBA, BEC and ACF are erected on the sides of any triangle ABC, and G, H and I are in the SAME RELATIVE¹ position to these triangles, then they form a triangle GHI similar to the three triangles.

Footnote: 1) If two triangles ABC and A'B'C are directly similar, then the point P' is in the same relative position to ΔA'B'C as P is to ΔABC if the transformation (in this case a translation or a spiral similarity) which maps ΔABC to ΔA'B'C, also maps the point P onto P'.

Napoleon Generalization 1 (1995)

*****

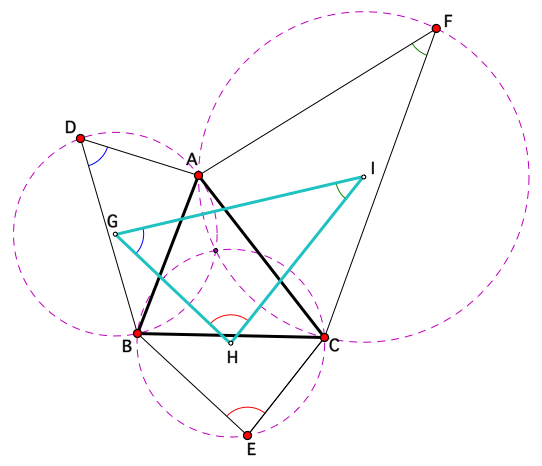
Generalization 2
a) If triangles DBA, BEC and ACF are erected on the sides of any triangle ABC, so that ∠D + ∠E + ∠F = 180^o, and G, H and I are the circumcentres, then ∠G = ∠D, ∠H = ∠E, and ∠I = ∠F, and the three circumcircles of the three triangles are concurrent.
b) To view & manipulate the dynamic version of this 2nd generalization, navigate to it by clicking on the 'Link to Generalization 2' button in the above dynamic sketch; the illustrative diagram below is static.
c) Another dynamic sketch illustrating this generalization is also available as 'Generalization of Napoleon's theorem' at: Some Circle Concurrency Theorems.

Napoleon Generalization 2 (1967)

Explore More: A Variation
a) Using Napoleon Generalization 2, the following different arrangement to the 3 similar triangles in Napoleon Generalization 1, for which the circumcentres would also give GHI similar to the 3 similar triangles is possible: If similar triangles DBA, CBE, and CFA are erected on the sides of any triangle ABC, their circumcenters G, H, and I form a triangle similar to the three triangles.
(This variation involving a different arrangement of similar triangles though given in De Villiers (1999) appears not to be well-known).
b) To view & manipulate a dynamic version of this arrangement of three similar triangles on the sides for which GHI is similar to the three outer triangles, navigate to it by clicking on the 'Link to Similar Triangles Variation' button '' in the dynamic sketch at the top.

Proving Generalization 2
While it's nice to prove Generalization 2 (and its two Similar Triangles Variation versions) with theorems from circle geometry as shown in Coxeter & Greitzer (1967) or De Villiers (1999, 195-196), the result about the angles of ΔGHI follows directly from Pompe's Hexagon Theorem (2016). Note that even though the latter theorem by Pompe doesn't directly prove the concurrency of the circumcircles, it can easily be derived from it as a corollary.

*****

A special case of Generalization 2: Miquel's Theorem
a) If the vertices of triangle ABC lie, respectively, on sides DF, DE and EF of ΔDEF, then the three circumcircles ADB, EBC and FCA are concurrent, and triangle GHI is similar to ΔDEF (Coxeter & Greitzer, 1967).
b) To view & manipulate the dynamic version of Miquel's Theorem, navigate to it by clicking 'Link to Special Case - Miquel' button in the dynamic sketch at the top; the picture below is static.

Napoleon Specialization (1967): Miquel's Theorem

Historical Note: This theorem was discovered by Miquel in 1838, and is sometimes also called the "Pivot" theorem. It's also easy to prove independently without the use of the above Generalization 2 of Napoleon - see for example: Miquel's Theorem (Rethinking Proof activity).

References
Coxeter, H. & Greitzer, S. (1967). Geometry Revisited, pp. 61-65. Washington: DC, MAA.
De Villiers, M. & Meyer, J. (1995). A generalized dual of Napoleon's theorem and some further extensions. Int. J. Math. Ed. Sci. Technol., 26(2), pp. 233-241.
De Villiers, M. (1994, 1996, 2009). Some Adventures in Euclidean Geometry (free to download). Lulu Press: Dynamic Mathematics Learning, pp. 177-179.
De Villiers, M. (1999, 2003, 2012). Rethinking Proof with Geometer's Sketchpad (free to download). Key Curriculum Press.
Pompe, W. (2016). Wokół obrotów: przewodnik po geometrii elementarnej. Wydawnictwo Szkolne Omega, Kraków, Poland.

Some Other Papers
John Rigby from the Math Dept, Cardiff University creatively uses tessellations in his 1988 paper Napoleon Revisited in the Journal of Geometry to prove Napoleon's theorem as well as some of the above generalizations.
Martini, H. & Weibbach, B. (1999). Napoleon's Theorem with Weights in n-Space. Geometriae Dedicata, 74, pp. 213–223.
Boutte, G. (2002). The Napoleon Configuration. Forum Geometricorum, 2, pp. 39-46.
Van Lamoen, F. (2003). Napoleon Triangles and Kiepert Perspectors. Forum Geometricorum, 3, pp. 65-71.
In a 2017 paper A generalization of the Napoleon's Theorem in Mathematical Reflections, no. 3, Khakimboy Egamberganov generalizes Napoleon's Theorem even further, and applies it to solve several interesting Olympiad type problems, including Pompe's Hexagon Theorem. In addition, Egamberganov's Theorem is a lovely generalization of Generalizations 1 & 2 above as well as of the Similar Triangles Variation Generalization.

Explore More
For other generalizations & variations of Napoleon, including Fox's theorem, and more on Egamberganov's Theorem, see Related Triangle Variations & Generalizations of Napoleon's Theorem.

Related Links
Napoleon's Theorem (Rethinking Proof activity)
The Fermat-Torricelli Point (Rethinking Proof activity)
Airport Problem (Rethinking Proof activity)
Weighted Airport Problem
Some Circle Concurrency Theorems (Approaching Napoleon differently)
Napoleon's Theorem: Generalizations, Variations & Converses
Napoleon's Regular Hexagon
Some Hexagon Generalizations of Napoleon's Theorem
Pompe's Hexagon Theorem (Provides a direct proof of Napoleon's theorem)
Sum of Two Rotations Theorem
Some Converses of Napoleon's Theorem Attached Regular Pentagons form Congruent Equilateral Triangles
Bride's Chair Concurrency & Generalization
Miquel's Theorem (Rethinking Proof activity)

A variation of Miquel's theorem and its generalization
Minimum Area of Miquel Circle Centres Triangle
Fermat-Torricelli Point Generalizations
Some Variations of Vecten configurations
Dirk Laurie Tribute Problem Generalizations (Asymmetric Propeller)
Parallelogram Squares (Rethinking Proof activity)
Van Aubel's Theorem and some Generalizations
The 120^o Rhombus (or Conjoined Equilateral Triangles) Theorem

Some External Links
Napoleon's theorem (Wikipedia)
Napoleon's Theorem, A Generalization (Cut The Knot)
Napoleon's Theorem (Wolfram MathWorld)
UCT Mathematics Competition Training Material
SA Mathematics Olympiad Questions and worked solutions for past South African Mathematics Olympiad papers can be found at this link.
(Note, however, that prospective users will need to register and log in to be able to view past papers and solutions.)

********************************