My site is entirely SAFE and FREE of viruses and spyware, but you might get an INSECURE SITE message from your browser simply because it is HTTP and not HTTPS.
Downloadable Articles, Papers & Materials
Michael de Villiers/Dynamic Mathematics Learning
........................
........................
Last Update: 26 June 2023
Updated: Math Ed Articles, Dynamic Geometry Sketches, Math e-Newsletter, Quote & Cartoon (at bottom)
...
...
...
...
...
Click on any of the above pictures for more information about these books and/or to purchase.
SKETCHPAD IS NOW FREE, and a copy can be downloaded from FREE SKETCHPAD (for Mac) or directly as a zipped file from FREE SKETCHPAD (for Windows) (after unzipping use the .exe file to install). You can then use any valid license code on 1, 2, 3, or 1,000 machines and Sketchpad will be fully functional on all those machines. When you are prompted, and you've forgotten or don't have a license code, use the License Name and Authorization Code provided below to unlock your license for Sketchpad. Use all characters and spaces as shown, including the 6-character code that appears at the end of the License Name.
License name: Pythagoras Single User License 1863 KJUJAM
Authorization code: BDFBF968
Click Fathom Demo to download a FREE DEMO of Fathom, the premier dynamic statistics package.
Bi-Annual Math e-Newsletter (Dec 2019)
Updated!!!Java Sketchpad, Cabri 3D, Cinderella & GeoGebra Sketches - interactive geometry on the web
Have a look at some of my geometry students' comments by clicking Feedback
For published reviews of my Rethinking Proof with Sketchpad book: Rethinking Proof Reviews
15% off Print Books till 25 February 2022 Downloadable PDF papers/books on Geometry, Mathematics & Mathematics Education for sale
NEW! Problem solving and logical thinking games for young children Contact dynamic learn @mweb. co. za (without the spaces) to order.
Most cited papers and books according to Google Scholar (27 June 2015):
1) The Role and Function of Proof in Mathematics (1990) - cited by 276.
2) Rethinking Proof with Sketchpad (1999/2003) - cited by 221.
3) The role and function of a hierarchical classification of quadrilaterals (1994) - cited by 116.
4) To teach definitions in geometry or teach to define? (1998) - cited by 103.
5) An Alternative Approach to Proof in Dynamic Geometry (1998) - cited by 101.
6) Using dynamic geometry to expand mathematics teachers' understanding of proof (2004) - cited by 60.
7) The Role of Proof in Investigative, Computer-based Geometry: Some Personal Reflections (1997) - cited by 57.
8) The Future of Secondary School Geometry (1996) - cited by 53.
9) The Role and Function of Quasi-empirical Methods in Mathematics (2004) - cited by 45.
PODCAST: Listen to the Podcast of my approx. 46 min Interview by Michelle Cirillo (University of Missouri) at ICME 13 in Hamburg in July 2016 about my career in Mathematics Education. (If problems are experienced playing it through completely in your browser, ensure that you have 'Allowed Flash Player' in your settings and preferences).
Free Articles/papers/talks
Please note that most of the articles/items below are in pdf format and require Adobe Acrobat Reader which can be downloaded for free from Adobe Acrobat Reader
The articles and materials below may be used for non-profit educational purposes only, provided that their source/origin is properly referenced at all times.
Kindly please inform me of any links or downloads that are NOT working properly.
Mathematics Education
NEW!!! Does dynamic computer verification imply the end of proof? My Plenary Talk via Zoom, 26 October 2021, 2nd NaCoME Conference organized by the Mathematics Education Study Program of Sriwijaya University, Indonesia.
A Diagonal Property of a Rhombus Constructed from a Rectangle in Learning & Teaching Mathematics, Dec 2018, pp. 26-27, PDF; co-author Jim Metz, Hawaii.
Tiling with a Trilateral Trapezium and Penrose Tiles Defines a "Trilateral Trapezium" and a "Triangular Kite" and then explores a tiling of respective special cases of these quadrilaterals, namely, a golden trilateral trapezium and its dual, a convex Penrose tile. Learning & Teaching Mathematics, March 2019, pp. 6-10, PDF.
Why does it Work? A Mathematical Explanation and Further Generalization of a Card Trick A card trick is mathematically explained using elementary school algebra and then generalized. Learning & Teaching Mathematics, Dec 2018, no. 24, pp. 30-31, PDF.
A cyclic Kepler quadrilateral and the Golden Ratio Defines a "Kepler quadrilateral" as a quadrilateral with sides in geometric progression of √φ, and proves an interesting property when it is cyclic. At Right Angles, March 2018, pp. 91-94, PDF. A dynamic geometry sketch is available online: click here to access.
An Example of Constructive Defining: From a Golden Rectangle to Golden Quadrilaterals and beyond Investigates different possible definitions for various 'golden' quadrilaterals that involve some aspect of the golden ratio. At Right Angles, Vol 6, no 1, March 2017, pp. 64-69; Vol 6 No 2, August 2017, 1.9 MB, PDF.
Reflecting on a 2nd Round 2013 SA Mathematics Olympiad Problem Presents a few different solutions as well as a more general underlying theorem. Learning & Teaching Mathematics, Dec 2013, No. 14, pp. 34-35, 193 KB, PDF. A dynamic geometry sketch is available online: click here to access.
A Multiple Solution Task: a SA Mathematics Olympiad Problem Explores some different solutions for a Round 1, South African Math Olympiad Problem from 2016. Learning & Teaching Mathematics, June. 2016, No. 20, pp. 18-20, 258 KB, PDF. A dynamic geometry sketch is available online: click here to access.
Order of Operations: The Math and the Myth Discusses why a well-defined order of arithmetic operations is needed, namely, to avoid ambiguity in interpreting a given number sentence. AMESA News, Nov. 2015, Vol. 57, pp. 9-11, 180 KB, PDF.
I have a dream ... Crossed Quadrilaterals: A Missed Lakatosian Opportunity? Initially presents some prose in the form of a critical satire of the still dominant practice in mathematics education to exclude crossed quadrilaterals from the set of quadrilaterals. The accompanying, follow-up paper briefly discusses this practice as a missed opportunity to engage students in a genuine Lakatosian experience. Philosophy of Mathematics Education Journal, July 2015. , 451 KB, PDF.
Slaying a Geometrical Monster: Finding the Area of a Crossed Quadrilateral. Discusses how to find the area of a crossed quadrilateral and to prove Varignon's theorem in the case when the quadrilateral becomes crossed. Scottish Mathematical Council Journal, 44 (Dec 2014), pp. 71-74; Learning and Teaching Mathematics, No. 18, June 2015, pp. 23-28, 332 KB, PDF. A dynamic geometry sketch is available online at Varignon's Theorem: the crossed case.
Conjecturing, refuting and proving within the context of dynamic geometry Two convincing geometry conjectures of points appearing to be collinear are given that easily pass a normal 'drag-test' with dynamic geometry software. Counterexamples only became evident after dilating the figures by a very large scale factor of about 100:1. Learning & Teaching Mathematics, Dec 2014, No. 17, pp. 20-26 pp, 795 KB, PDF. Co-author: Nic Heideman. Dynamic geometry sketches available online at Investigating incentres of some iterated triangles.
Over and over again: two geometric iterations with triangles Presents and proves two interesting geometric iterations that converge to equilateral triangles. Suitable dynamic geometry exploration for Grade 10-12 learners and up. Learning & Teaching Mathematics, July 2014, No. 16, pp. 40-45, 426 KB, PDF. Dynamic geometry sketches available online at Over and over again: two geometric iterations.
Learners' conceptualisation of the Sine function during an introductory activity using Sketchpad at Grade 10 level Discusses research that revealed some intuitions as well as misconceptions about the sine function. Presented by Janeeshla Jugmohan at the Educational Society of South Africa (EASA) Congress, Univ. of KwaZulu-Natal, 13-16 January 2009.
A Trapezium Theorem Generalized Generalizes the so-called Midpoint Trapezium Theorem to a simple inequality for any quadrilateral. Suitable exploration for Grade 9-10 learners and up. At Right Angles, Nov 2013, Vol. 2, No. 3, pp. 53-56, 213 KB, PDF. Dynamic geometry sketches available online at Midpoint Trapezium Theorem Generalized.
A dynamic approach to quadrilateral definitions By Rajendren Govender and Michael de Villiers. This study found that the evaluation of different definitions for a rhombus by accurate construction and measurement in a dynamic geometry context, enabled prospective mathematics students to achieve a better understanding of necessary and sufficient conditions, as well as the ability to more readily find counter-examples, and to recognise and improve on uneconomical definitions. Pythagoras, 2004, No. 58, pp. 34-45, 238 KB, PDF
Competencies in using Sketchpad in Geometry Teaching and Learning: Experiences of preservice teachers By Mdutshekelwa Ndlovu, Dirk Wessels and Michael de Villiers. Describes some qualitative research used to investigate preservice teachers' emerging competencies. African Journal of Research in Mathematics, Science and Technology Education, 2013, Vol. 17, No. 3, 231-243, 479 KB, PDF
Equality is not always best! Describes a classroom discussion which revealed the surprising discovery that the circumcentre is perhaps not the 'best choice' for building a water reservoir for 3 villages lying in the shape of an obtuse triangle, despite the circumcentre being equi-distant from all 3 villages. A 'better' solution is then presented. Learning & Teaching Mathematics, no. 14, June 2013. pp. 17-21, 397 KB, PDF
What is the function? Models the height of water being poured into a tilted container in a video clip with a simple differential equation to find the function. Learning & Teaching Mathematics, no. 12, June 2012. pp. 16-18, 418 KB, PDF
An Example of the Explanatory and Discovery Functions of Proof My ICME 12 invited, regular paper discusses a variation of Viviani's theorem, originally suggested by a high school student, and how reflecting - looking back - on different proofs of the result leads to various different generalizations. Pythagoras, 33(3), Dec 2012. 8 pp, 639 KB, PDF
An Alternative Approach to Proof in Dynamic Geometry Chapter in 1998 Erlbaum book Designing Learning Environments for developing Understanding of Geometry and Space, edited by Richard Lehrer and Daniel Chazan. It critiques the traditional approach to proof which focusses mainly on the verification function of proof, and argues for an alternative, more meaningful introduction to proof, specifically in the context of dynamic geometry, by focussing on the explanatory function of proof. 25 pp, 5.3 MB, PDF
An instrumental approach to modelling the derivative in Sketchpad Discusses a hypothetical learning trajectory for modelling the derivative and related concepts in introductory calculus with dynamic mathematics software, and which was implemented with first-year non-mathematics major undergraduate science students., Ndlovu, M., Wessels, D., & De Villiers, M. (2011). Pythagoras, 2011, 3.8 MB, PDF
Simply Symmetric Briefly discusses and illustrates the value of symmetry in choice of definitions in geometry and in problem solving, Mathematics Teaching; Teaching and Learning Math, 2011, 303 KB, PDF
Worksheet: Order of operations Worksheet and Teacher Notes to develop understanding of the need for 'order of operations' in order to avoid 'ambiguity', Pythagoras, 1992, 1.9 MB, PDF
2010 Van Hiele plenary paper now available in Portuguese & Croatian
A Comparative Study of two Van Hiele Testing Instruments Poster paper presented by a then student of mine, Eddie Smith, at PME-13, Paris 1989
Some Reflections on the Van Hiele theory. Invited paper and video made at the Program Post-Graduate Studies in Mathematics Education at the Pontifical Catholic University of Sao Paulo, Brazil in April 2010, as well as invited plenary at the Croatian Mathematical Conference in Zagreb, Croatia in June 2010
Border Patterns, Tessellations & Problem Solving with Transformations. Invited paper AMESA Congress, 2007, 1.1 MB, PDF
Research Evidence on Hierarchical Thinking, Teaching Strategies and the Van Hiele Theory: Some critical comments. RUMEUS Report, pp. 36, 1987, 1.5 MB, PDF
ICMI-19 Discussion Document: Proof and Proving in Mathematics Education. pp. 12, 2007/8, 136 KB, PDF
Problemsolving and Proving via GeneralizationLearning & Teaching Mathematics, no. 5. pp. 19-25, 2008, 900 KB, PDF
Mathematical Applications, Modeling and TechnologyInvited Plenary at Annual Congress of AMESA, July 2007, AMESA Proceedings, 1.2 MB, PDF
Some pitfalls of dynamic geometryDiscusses some pitfalls of using dynamic geometry in teaching geometry. Feb 2007, Teaching & Learning Mathematics, 276 KB, PDF
Recycling cyclic polygons dynamicallyThis article includes zipped Sketchpad sketches and deals with testing by construction, and proving the converse of a well-known cyclic quad theorem, and then considering some generalizations. May 2006, Mathematics in School, 64 KB.
Rol en Functie van het Bewys in de Dynamische Meetkunde (A somewhat modified and translated version into Dutch of my "Role & function of proof in Dynamic Geometry", pdf, 300 KB, EUCLIDES, Feb 2006, 81(4), pp. 184-188)
Mathematical Modeling and Proof (pdf, 24 KB, AMESA '04 paper)
Using dynamic geometry to expand mathematics teachers' understanding of proof, 2004, IJMEST 35 (5), pp. 703-724, 176 KB
Clough's Conjecture - A Sketchpad Investigation (Workshop on a variation of Viviani's theorem presented at AMESA 2004, Potchefstroom & NCTM 2004, Philadelphia.
Rethinking Proof with Sketchpad - in Hebrew (pdf, 2003 in ALEH, 30, May, 19-26. English versions are in ARCHIVE articles below)
A further Pythagorean Variation on a Fibonacci theme (MiS, 2002, pdf)
All cubic polynomials are point symmetric (TLM, 2004, pdf)
The Role and Function of a Hierarchical Classification of Quadrilaterals (FLM, 1994, pdf)
The role of experimentation in mathematics (AMESA 2003 paper)
A Sketchpad Investigation of "Arithmetic Sequence" Parabola (AMESA 2003 Workshop)
Developing understanding for different roles of proof in dynamic geometry (ProfMat 2002, pdf)
Para uma Compreensao dos Differentes Paeis La Demonstracao em Geometria Dinamica (ProfMat 2002, pdf)
The Role and Function of Proof with Sketchpad (1999, pdf)
Constructive Evaluation of Definitions in a Sketchpad Context (Amesa 2002 paper, pdf file)
Mathematics
NEW!!! An Interesting Collinearity Learning & Teaching Mathematics, July 2019. No. 26, pp. 28-30, PDF. (Co-author: Piet Human). An application of Desargues and Pappus. A dynamic geometry sketch is available online: click here to access.
A surprising 3D result involving a hexagon Mathematical Gazette, July 2018. 2018, Vol. 102, No. 554, pp. 328 - 330, PDF. A link to a YouTube video giving a 3D illustrations of the result is available online: click here to access.
A Merry-Go-Round the Triangle Illustrates the value of problem-posing, e.g. how asking a 'what-if' question leads to an interesting result. Learning & Teaching Mathematics, June 2018, No. 24, pp. 17-20, 446 KB, PDF. Co-author: John Silvester. A dynamic geometry sketch is available online: click here to access.
A Multiple Solution Task: Another SA Mathematics Olympiad Problem Explores some different solutions for a Round 2, South African Math Olympiad Problem from 2016. Learning & Teaching Mathematics, June 2017, No. 22, pp. 42-46, 464 KB, PDF. A dynamic geometry sketch is available online: click here to access.
Enrichment for the Gifted: Generalizing Some Geometrical Theorems & Objects (pdf, 385 KB, 2016 in Learning and Teaching Mathematics (Dec)). This ICME 13 presented paper discusses the importance of encouraging generalization in mathematics as well as engaging learners in constructive defining. A dynamic geometry sketch related to the generalization of a rectangle to a hexagon is available online at Dynamic sketch.)
Flashback to the Past: a 1949 Matric Geometry Question (pdf, 713 KB, 2015 in At Right Angles (Nov) and Learning and Teaching Mathematics (Dec)). This paper explores a 1949 Grade 12 Geometry Exam question, by looking at a generalization and some variations. A dynamic geometry sketch is available online at Dynamic sketch.)
A trisection concurrency: a variation on a median theme (pdf, 881 KB, Learning and Teaching Mathematics, Dec 2013, pp. 36-40). Co-author: Shunmugam Pillay. Or alternatively, download and read in iBook format (2 MB). This result deals with an interesting concurrency found experimentally when the sides of a triangle were trisected, its proof and further generalization. A dynamic geometry sketch is available online at Dynamic sketch.)
A variation of Miquel's theorem and its generalization (pdf, 233 KB, Mathematical Gazette, July 2014, pp. 334-339. This note describes a little known 'converse-like' variation of Miquel's theorem and its generalization to higher polygons. Dynamic geometry sketches are available online at Dynamic sketches.)
Quasi-circumcenters and a Generalization of the Quasi-Euler Line to a Hexagon (pdf, 45 KB, Forum Geometricorum, Vol 14(2014), pp. 233-236. This short note generalizes the quasi-Euler line of a quadrilateral to a hexagon involving its quasi-circumcenter, its quasi-orthocenter and its lamina centroid. Dynamic geometry sketches are available online at Dynamic sketches.)
An Investigation of Some Properties of the General Haag Polygon (pdf, 553 KB, Mathematics in School, 43(3), May 2014, pp. 15-18. Investigates the generalization of some angle and concurrency properties of the tessellating Haag hexagon. Dynamic geometry sketches are available online at Dynamic sketches.)
Generalizing a theorem of Arsalan Wares (pdf, 279 KB, The Scottish Mathematical Council Journal, no. 42, 2012, pp. 41-43. Presents some generalizations of Wares' theorem - involves similar triangles. Dynamic geometry sketches are available online at Dynamic sketches.)
3D Generalizations of Viviani's theorem (pdf, 385 KB, The Mathematical Gazette, Vol, 97, no. 540, Nov 2013, pp. 441-445. Presents some 3D generalizations of Viviani's theorem. Dynamic geometry sketches with Cabri 3D (for Windows only - download required plug-in) are available at Dynamic 3D.)
LTM Feb 2006 Cover Diagram: A semi-regular side-gon (pdf, 287 KB, Learning & Teaching Mathematics, no. 12, June 2012, pp. 34-35. Discusses some mathematical properties of the semi-regular octagon on the 2006 cover of the LTM journal.)
Another proof of De Opgave 2011 (pdf, 164 KB, Euclides, Dec 2012. Provides another proof of a geometry problem posed by Dick Klingens in 2011, and relates it also to a generalization of Van Aubel's theorem.)
Relations between the sides and diagonals of a set of hexagons (pdf, 586 KB, Mathematical Gazette, July 2012. Explores the analogous case for parallelo-hexagons of the parallelogram theorem that the sum of the squares of the sides of a parallelogram is equal to the sum of the squares of its diagonals.)
Generalizing a problem of Sylvester ( pdf, 258 KB, Mathematical Gazette, March 2012. Generalizes Sylvester's result that the resultant of three equal forces OA, OB and OC acting on the circumcentre O of a triangle ABC, is the force represented by OH, where H is the orthocentre of the triangle.)
Equi-angled cyclic and equilateral circumscribed polygons ( pdf, 565 KB, Mathematical Gazette, 2011. Generalizes rectangles and rhombi to higher polygons.)
From the Fermat points to the De Villiers points of a triangle ( pdf, 1.2 MB, AMESA Congress July 2009 paper. Describes the discovery and proof of the so-called De Villiers points of a triangle, tracing its origin from the Fermat points of a triangle.)
Vanaf die Fermat punte na die De Villiers punte van 'n driehoek ( pdf, 344 KB, SA Tydskrif vir Natuurwetenskap & Tegnologie, Sept 2010. Beskryf die ontdekking en bewys van die sogenaamde De Villiers punte van 'n driehoek, en trek die oorsprong terug na die Fermat punte van 'n driehoek.)
Some hexagon area ratios: Problem solving by related example ( pdf, 324 KB, Mathematics in School, 2010. Describes the discovery and proof of an interesting area ratio result for a parallelo-hexagon.)
Generalizing the Nagel line to Circumscribed Polygons by Analogy & Constructive Defining (pdf, 548 KB, Pythagoras, 2008. First discusses the genetic approach & the importance of the history of math, reasoning by analogy, and the role of constructive defining before presenting the result - with downloadable GSP sketch.)
LTM Cover Problem ( pdf, 248 KB, Learning & Teaching Mathematics Journal, 2009. Gives a proof of the result, and two additional problems - with links to interactive sketches.)
A Further Generalization of Turnbull's Theorem ( pdf, 464 KB, IJMEST, 1993. Generalizes the familiar "opposite angle supplementary" theorem for cyclic quadrilaterals to other cyclic polygons.)
Solving a Locus Problem via Generalization (Contains link to a Sketchpad sketch, pdf, 20 KB, Reflections, Spring 2008, pp. 20-21. Applies circle geometry and similarity to solving a locus problem.)
A Question of Balance: An Application of Centroids (Contains link to a Sketchpad sketch, pdf, 416 KB, Mathematical Gazette, Nov 2007, pp. 525-528, and March 2008. Applies similarity and centroids to proving a result about similar quadrilaterals on the sides of a quadrilateral.)
An example of the discovery function of proof(Contains link to a Sketchpad sketch, pdf, 32 KB, Mathematics in School, Sept 2007, pp. 9-11. Generalizes a 9th grader's discovery for a triangle to a convex quadrilateral.)
A hexagon result & its generalization via proof(Contains link to a Sketchpad sketch, pdf, 88 KB, The Montana Mathematics Enthusiast, June 2007, Vol. 4, No. 2. Illustrates the discovery function of proof by generalizing a hexagon result.)
Further Reflection on a SA Mathematics Olympiad Problem(Contains link to a Sketchpad sketch, pdf, 40 KB, Learning & Teaching Mathematics, March 2007, pp. 25-27. Discusses underlying hidden theorem related to a special type of quadrilateral, and how this in turn can be viewed as a special case of Dandelin's Theorem.)
More on hexagons with opposite sides parallel (Contains link to a Sketchpad sketch, pdf, 120 KB, Mathematical Gazette, Nov 2006)
A generalization of the Spieker circle and Nagel line (Contains link to Sketchpad sketches, pdf, 100 KB, Pythagoras, July 2006)
A generalization of the Nine-point circle and Euler line (Contains links to Sketchpad sketches, a further generalization of the Euler line and a synthetic proof, pdf, 40 KB, Pythagoras, Dec 2005)
The nine-point conic: a rediscovery and proof by computer (Describes a generalization of nine-point circle and associated Euler line & proof by computer, pdf, 216 KB, IJMEST, Jan 2006)
Feynman's Triangle: Some feedback and more (pdf, 16 KB, Math Gazette, March 2005)
A dual to a BMO problem (pdf, 12 KB, March 02 Math Gazette)
Ezit's Rule: An Explanation & Proof (From LTM, Feb 2005, PDF, 20 KB)
An Extended Classification of Quadrilaterals (An excerpt from my Some Adventures In Euclidean Geometry booklet, 8 KB, pdf)
Crocodiles and Polygons: A generalization of Viviani's theorem to equi-angled polygons. An article from March 2005 issue of Mathematics in School, pdf.
Stars: A Second Look (Pdf, A 1999 article in Math in School as a short response to another article on the interior angle sum of star polygons.)
An interesting property of a quadrilateral circumscribed around a circle. (An excerpt from my book Some Adventures in Euclidean Geometry, 1996, pdf.)
'n Bewys deur matematiese induksie van 'n bekende bewering - in Afrikaans (jpg, 1988, . Spectrum 26(3), August, p.38. (Will be rewritten in English at some stage & posted here. Alternatively, read Alwyn Olivier's classroom notes (1999), which deals (among others) with the same result, at: Circles, Regions and Chords).
A Fibonacci Generalization and its Dual (2000, IJMEST, pdf)
Generalizations of maltitudes (IJMEST, 1999, pdf) (includes a generalization of Euler line to cyclic polygons)
The Affine Equivalence of Cubic Polynomials (2003, pdf)
How does the wind affect road-running achievement? (1991, pdf)
From Miquel Triangles to Miquel Distances (2002, pdf)
Dual Generalizations of Van Aubel's Theorem (pdf)
A Generalization of the Fermat-Torricelli Point (pdf)
A Further Generalization of the Fermat-Torricelli Point (pdf)
More articles
Please click on the links below for more of my older articles & publications.
ARCHIVE OF MATHEMATICS EDUCATION (Articles uploaded earlier; e.g. Role of Proof - also in Spanish & Portuguese; Teaching Definitions; Future Of Secondary School Geometry - also in Spanish; Role of Technology in Math, etc.)
ARCHIVE OF MATHEMATICS (Articles uploaded earlier; e.g. on theorems of Van Aubel, Kosnita, Haruki, side-angle duality, applications in rugby, tennis; etc.)
SKETCHPAD COMPETITION SOLUTIONS
READER INVESTIGATIONS from KZN AMESA MATHEMATICS JOURNAL
Sketchpad Sketches
Experience the POWER and BEAUTY of moving geometric figures; i.e. DYNAMIC GEOMETRY!
Download FREE Sketchpad 3 sketches for investigations or demonstrations by clicking on SKETCHPAD 3 SKETCHES
Download FREE Sketchpad 4 sketches for investigations or demonstrations by clicking on SKETCHPAD 4 SKETCHES
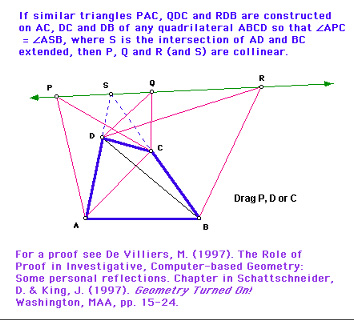
Dynamic Geometry sketches for my paper THE ROLE OF PROOF IN INVESTIGATIVE, COMPUTER-BASED GEOMETRY: SOME PERSONAL REFLECTIONS in the MAA Book "Geometry Turned On: Dynamic Software in learning, Teaching, and Research", 1997, edited by James King & Doris Schattschneider (as well as other sketches & files from the book) can be found at geometry turned on
Free 12 pp booklet BUILDING RELATIONSHIPS: UNCOVERING MATH WITH YOUR FAMILY is available from Texas Instruments and can be downloaded from family math
ASSOCIATION FOR MATHEMATICS EDUCATION OF SOUTH AFRICA(AMESA)
MATHEMATICIANS BORN OR DIED TODAY and other history of math
GEOMETRY STEP BY STEP FROM THE LAND OF THE INCAS
FIBONACCI A site on FIBONACCI numbers and the GOLDEN SECTION is a useful resource for encouraging students into math.
Find out about latest developments in mathematical research. Written for the layperson. What's New in Mathematics
Comprehensive List of Links to Math Sites
Cartoon
Quote of the Month
Contact me at: profmd @ mweb.co.za (use without spaces)
